Rayon de convergence

[phuor]

Bonsoir,
Je n'arrive pas à résoudre l'exercice suivant:
On se donne z0 et K >= 0, k >=0 tq |a0 + a1z0 + ... + anz0^n| < K n ^k.
Montrer que le rayon de convergence de la série de terme anz^n est plus grand que |z0|.

Besoin d'aide car je ne vois pas comment arriver à démontrer en partant du module de la somme en z0.

merci d'avance.

[girdav]

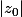
On a par l'inégalité triangulaire que . Si le rayon de convergence est strictement plus petit que , alors on peut trouver tel que ne soit pas bornée. On a
pour tout entier , une contradiction.

[phuor]

Bonsoir,

je ne comprends pas comment qu'en partant des inégalités triangulaires et du module de |a+a1z0+...anz0^n|
merci

[raito123]

Bonsoir,

je ne comprends pas comment qu'en partant des inégalités triangulaires et du module de |a+a1z0+...anz0^n|<Kn^k tu arrives à |anz0^n| < 2Kn^k.

merci

On a bien d'après l'inégalité triangulaire renversée

[bentaarito]

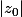
On a par l'inégalité triangulaire que . Si le rayon de convergence est strictement plus petit que , alors on peut trouver tel que ne soit pas bornée. On a
pour tout entier , une contradiction.

C'est plutôt

pour tout entier

qui mène à une contradiction :lol3:

[cuati]

C'est plutôt

pour tout entier

qui mène à une contradiction :lol3:

Oui effectivement, mais bon, on avait compris... bravo Girdav.

[phuor]

Bonjour,
merci à vous.
Il est vrai que le terme de rang n est la difference de deux sommes.
Et encore bravo!

[girdav]

C'est plutôt

pour tout entier

qui mène à une contradiction :lol3:

Oui, merci de m'avoir signalé la faute de frappe.

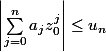
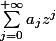
Il me semble, mais je peux me tromper, que l'on peut généraliser : si est une suite croissante telle que si , et si pour tout , alors le rayon de convergence de la série est au moins égal à .

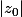
Ou alors, on peut se passer de l'hypothèse de croissance si pour tout .