Rayon cercle incrit

par **Elise68** » 19 Avr 2009, 20:39

Bonjour tout le monde,

J'ai juste une petite question..
Connait-on une relation entre les rayons du cercle inscrit et circonscrit?
Je lisais un corrigé d'exercice où on avait un triangle equilatéral et il était utilisé que le rayon du cercle inscrit était la moitié de celui du cercle circonscrit, alors je me demandais juste comment le montrer!
Voilà, merci d'avance !

par **Ericovitchi** » 19 Avr 2009, 21:27

Si I est le centre du cercle inscrit et O le centre du cercle circonscrit on a

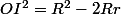C'est encore Euler qui a trouvé ça.

Sinon je connais le théorème dit de Lazare Carnot :
La somme des distances du centre du cercle circonscrit aux cotés du triangle est égale à la somme du rayon du cercle circonscrit + rayon du cercle inscrit
OO1+OO2+OO3=R+r

Et tout ça c'est vrai pour un triangle quelconque alors pour un triangle équilatéral, ca va s'améliorer beaucoup (OI=0 donc R=2r)

par **Zweig** » 19 Avr 2009, 21:30

Attention, pour le théorème de Carnot, ce sont les distances signées !

par **Zweig** » 19 Avr 2009, 21:37

On en a d'autres :

Soit ABC un triangle avec AC = b, BC = a et AB = c,

,

et

les rayons des cercles exinscrits respectivement aux côtés a, b et c du triangle, p le demi périmètre. Alors :

avec égalité lorsque le triangle est équilatéral

par **Elise68** » 20 Avr 2009, 11:16

Merci beaucoup pour votre aide :)

Rayon cercle incrit

rayon cercle incrit

Qui est en ligne