Raisonnement sur les matrices

[barbu23]

Bonsoir, :happy3:

Est ce que les matrices de permutations ( d'ordre par exemple ) sont co-diagonalisables dans leur ensemble ? En d'autres termes, est ce qu'il existe une base commune dans laquelle ces matrices de permutation sont toutes diagonales ?

Merci d'avance.

Edit : Sur le net, j'ai trouvé le théorème suivant sans démonstration malheureusement :
Soit une famille d'endomorphismes diagonalisables qui commutent. Alors, il existe une base qui diagonalise tous les éléments de la famille. Connaissez vous la démonstration de ce théorème ?
Merci d'avance. :happy3:

Edit : Y'a -t-il une méthode générale qui permet par induction de diagonaliser toutes les matrices de permutation comme c'est le cas des matrices circulantes ?
Merci d'avance. :happy3:

[barbu23]

Bonjour, :happy3:

Si on permute les coefficients d'une matrice diagonale de manière circulaire, est ce que cela veut dire qu'on a multiplié cette matrice diagonale par une matrice de permutation circulaire ( matrice circulante ) à gauche et à droite ?

Merci d'avance. :happy3:

[barbu23]

Bonjour à tous, :happy3:

On adopte tout d'abord les notation suivantes : et .
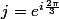
Et on considère l'équation suivante :

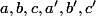
avec et sont les indéterminées.
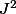
Est ce qu'il y'a un moyen de se débarrasser du facteur de façon à aboutir une écriture simplifiée de la forme :

Pour pouvoir avoir à la fin :

?

Merci d'avance. :happy3: