Raisonnement sur les matrices

[barbu23]

Bonjour à tous,

J'aimerais savoir si le raisonnement suivant est juste :
Je dispose du système suivant :

que je mets sous la forme suivante :

Cela équivaut à :


Jusqu'ici tout va bien :
Il existe matrices de permutations qui font permuter les valeurs qui se situent sur la diagonale d'une matrice, de sorte que :


équivaut à :



Question :
Est ce que : et et commutent entre elles de façon à simplifier :


en une écriture équivalente comme suit :


Merci d'avance. :happy3:

[adrien69]

Hmmm...
Ça se calcule bien ça.

et par exemple.

Donc après il n'y a plus qu'à vérifier que ça marche pour tout type de matrice diagonale.

[barbu23]

Merci, mais tu ne m'as pas dit si on peut faire commuter les matrices dont je vous ai parlé dans le message initial. :happy3:
Merci d'avance. :happy3:

[adrien69]

Ah ben ça je te laisse faire le calcul !
Ça prend 5 ou 6 lignes, c'est trop pour moi ^^





Franchement tu n'as plus qu'à faire le calcul avec des matrices diagonales quelconques au lieu des tiennes pour voir si ça marche ou pas.

[barbu23]

Moi aussi c'est trop pour moi ce calcul là. ^^
Moi, je veux savoir juste si le raisonnement est correct sans faire de calcul pour s'en convaincre. :happy3:

[barbu23]

svp, j'ai besoin de votre aide. :happy3:

[barbu23]

@adrien :
En fait, je cherche à appliquer des permutations seulement des valeurs qui se situent sur la diagonale d'une matrice. Avec les matrices que tu proposes, je ne pense pas que ça soit le cas. :happy3:

[Ben314]

Pour "permuter les valeurs sur la diagonale" comme tu dit, ben il suffit bètement de faire un changement de base en changant l'ordre des vecteurs) et, calculatoirement parlant, ça se fait en multipliant à droite par une certaine matrice P (de permutation) et à droite par son inverse.
Avec ça, tu n'a pas besoin d'intruduire tes truc complètement bizares avec lesquel on ne risque pas de faire de calculs...

[adrien69]

Rassure-moi, c'est bien ce que j'ai fait non ?

[Ben314]

Rassure-moi, c'est bien ce que j'ai fait non ?

Ben... plus ou moins vu que si tu regarde dans le détail ce que barbu à écrit, pour lui l'opération consistant à permuter les termes de la diagonale d'une matrice, il écrit ça comme un espèce d'opérateur qu'on met devant la matrice (et qui n'est donc pas lui même une matrice...)

Edit : En fait, c'est pas clair : il écrit que ces P_truc sont des matrices de permutations, mais la ligne d'en dessous, t'as pas vraiment l'impression qu'il utilise ces matrices là comme des matrices de changement de base : il ne semble pas multiplier à droite par l'inverse de ce qu'il a mis à gauche...

[adrien69]

J'ai sous-compris que c'était les inverses à droite, d'où le carré, mais bon.

[barbu23]

Salut à tous :
Non, voiçi mon raisonnement du début à la fin :


équivaut à :


C'est à dire :


Parce que : et
Par commutativité ( Si commutativité est valable ( C'est la question que je me pose bien entendu ) ) :


qui équivaut à :


C'est à dire :


Par commutativité également, on obtient :


Cela équivaut à :



C'est à dire :



Par commutativité également, on obtient :


Cela équivaut à :


C'est à dire :


Voiçi donc la fin du raisonnement. Ma question est donc de savoir s'il y'a commutativité dans le cas que j'ai appliqué.

Merci d'avance. :happy3:

[Doraki]

Si tout ce que tu fais c'est faire commuter des matrices diagonales, ça va. Mais j'ai pas l'impression que c'est ce que tu fais alors non.

C'est quoi comme matrices Pid, Pid-1, Psigma1, Psigma2, Ptau1 et Ptau2 ? (et y'a pas de Ptau3 ?)

[adrien69]

En fait je crois que tu ne comprends pas que pour i=1 ou 2 tu as et que les matrices sont alors données par ce que j'ai écrit.

Je ne vois pas pourquoi tu t'évertues à ne pas regarder explicitement, par un calcul, si les transformations que tu veux, et dont je t'ai donné la représentation, sont compatibles avec la commutativité.

[barbu23]

Si tout ce que tu fais c'est faire commuter des matrices diagonales, ça va. Mais j'ai pas l'impression que c'est ce que tu fais alors non.

C'est quoi comme matrices Pid, Pid-1, Psigma1, Psigma2, Ptau1 et Ptau2 ? (et y'a pas de Ptau3 ?)

Non, il n'y'a pas de .
( C'est la matrice identité qui vaut la permutation triviale : pas de permutation )
Quant à , , et ce sont des matrices de permutation relativement à une permutation que je ne cherche pas à identifier pour le moment. Je cherche juste à savoir si on peut appliquer la commutativité pour le moment. :happy3:
Si tu veux savoir à quoi elles sont égales ces matrices de permutation, tu peux les en déduire à partir des transformations qui se trouvent dans le message initiale. :happy3:

[barbu23]

En fait je crois que tu ne comprends pas que pour i=1 ou 2 tu as et que les matrices sont alors données par ce que j'ai écrit.

Je ne vois pas pourquoi tu t'évertues à ne pas regarder explicitement, par un calcul, si les transformations que tu veux, et dont je t'ai donné la représentation, sont compatibles avec la commutativité.

D'accord, je comprends l’intérêt de ce que tu dis, mais pour le moment, je cherche juste à comprendre si on a droit de permuter les facteurs comme cité dans le message précédent. :happy3:

[Doraki]

Peut-être que je dis un truc très stupide, mais est-ce que ce serait possible, pour savoir si deux matrices A et B commutent, de calculer A, B, AB et BA ???!!?!? Tu attends qu'on fasse le calcul à ta place ?

[barbu23]

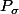
D'accord, j'essayerai de faire le calcul tout seul dans quelques instants, mais pour faire court, j'aimerais pouvoir me débarrasser des matrices de permutation , de façon à avoir à la fin une écriture de la forme :

que ce soit à l'aide de l’astuce de commutativité ou bien à l'aide d'une autre astuce qui peut se présenter par hasard.
Merci d'avance pour votre aide.

[Doraki]

Ton système inital est un truc de la forme (a1a2a3,b1b2b3,c1c2c3) = X.
Je ne vois pas par quelle sorte de miracle tu t'attends à ce que ce soit équivalent à un système de la forme (a1b3c2,a2b1c3,a3b2c1) = Y

[barbu23]

Oui, mais qui ne tente rien n'a rien. :zen: