Raisonnement logique

[hmz25]

bonjour a vous, ca fait un moment que je block sur ce raisonnement : « a vrai <==> b vrai » c'est de determiner
a est vrai si seulement b est vrai et b est vrai si seulement a est vrai et la solution c'est bien de supposer a vrai et déduire b est vrai et voila je ne voit pas pourquoi l'étape 2 est nécessaire en supposant b est vrai et déduire que a est vrai parce que dans le premier cas on a bien supposer a est vrai et on a déduit que b est vrai alor je conclu que quand b est vrai alor a est vrai et quand a est vrai b est vrai mais j'ai trouvé un exemple celui d'une chevre et son petit bébé et je me suit dit que pour que le bébé (de la chevre) existe(veut dire qu'il est vivant) il faut que la chevre existe
et pour prouver que la chevre existe il faut prouver que son petit bébé existe et je me suit dit on suposant que le bébé existe et on démontrant que la chevre existe et la je me suit dit que si la chevre existe elle peut ne pas avoir de bébé donc pour que léquivalence soit vrai il faut en fait supposer que la chevre existe et on déduire que le bébé existe.donc j'ai conclu que la 2 étape est nécessaire mais voila je suis un peu douteux je ne sais pas c'est un bon exemple (un exemple générale) ou c'est faut depuis le début voila j'éspere vraiment votre aide et merci a vous .

[Skullkid]

Bonjour,

Sans même prendre d'exemple,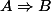 peut s'interpréter comme "A entraîne B". Normalement tu dois voir immédiatement que ce n'est pas la même chose que "B entraîne A". L'équivalence te dit que A entraîne B et B entraîne A. Donc si tu prouves juste que A entraîne B, tu n'as pas prouvé l'équivalence.

Sinon, essaye de faire un effort sur la ponctuation, ton post est vraiment pénible à lire...