Radical d'un idéal

[elaich]

Bonjour, voilà c'est mon premier poste ici ^^ je bloque là sur un petit truc:
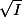
Soit un idéal de . on désigne par l'ensemble
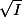
1) Montrer que est un idéal de
2) Soit un idéal de . Vérifier les règles de calcul suivantes:
a) et
b)
c)
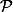
3) Montrer que si est un idéal de , alors et
4) Soit un entier >1. Déterminer .

Voilà où je suis:
1) alors il n'est pas vide, on prenons on a:
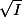
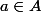
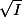
donc alors d'où est un sous-groupe commutatif de pour la loi + , d'autre part soit et on alors alors donc est un idéal de .

2)a) soit alors donc tel que et or:
car et est un idéal de même , donc
je bloque pour
Merci

[ThSQ]

C'est tout bête je crois :

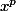
est inclus dans I donc si est dans il est dans I.

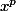
Maintenant si est dans I, est dans

[elaich]

C'est tout bête je crois :

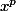
est inclus dans I donc si est dans il est dans I.

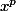
Maintenant si est dans I, est dans

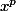
pourquoi tu prend les élément de sont de la forme avec

[nonam]

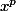
Il prend dans , car il suppose x dans le radical de

[ThSQ]

C'est tout bête je crois

C'est même encore plus bête (j'avais pas lu les autres questions), ça découle directement de



Bonus track : quels sont les éléments nilpotents de A/I :hum: :id: