[Algebre] radical d'un ideal

par **parisien75** » 28 Sep 2007, 20:11

Bonsoir.

Je cherche à déterminer le radical d'un idéal de l'anneau des polynomes à coéfficients dans

.

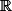
L'anneau des polynomes a coeff dans

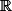
etant principal, j'en deduit que les idéaux de cet anneaux sont du type I = (P) avec P polynomes à coeff réels.

Donc

| il existe n

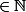
| Q^(n)

Ainsi

| il existe n

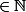
& S

|Q^(n)=P.S } puisque S

I

Je ne vois pas pour ou continuer

Si qqun aurait une petite idée, ce serait pas de refus.

Merci

par **fahr451** » 28 Sep 2007, 20:17

bonsoir

sauf erreur pour I = (P)

radical (I) = { Q tel que toute racine complexe de P est racine de Q}

par **parisien75** » 28 Sep 2007, 20:18

Sais tu grossièremeent comment arriver à ce resultat?

par **fahr451** » 28 Sep 2007, 20:24

grossi modo je sais

soit Q dans Radical(I)

il existe n

Q^n = PS donc toute racine complexe de P est racine de Q^n donc de Q

réciproquement

soit P = a(X-z1)^n1.....(X-zr)^nr

la factoriqationde P dans C
et Q telle que tous les zi sont racines de Q

il est clair que P divise Q^(max (ni)

[Algebre] radical d'un ideal

[Algebre] radical d'un ideal

Qui est en ligne