Racine rationnelle d'un polynôme à coef entiers

par **melreg** » 07 Fév 2008, 09:54

Bonjour,

Voici le problème :
Soit

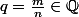
(on peut supposer la fraction irréductible) tel que q est racine du pôlynome

,

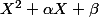
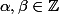
. Alors

...

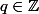
Moi, je n'arrive à rien!

par **yos** » 07 Fév 2008, 11:10

Bonjour.
Remplace X par m/n, multiplie les deux membres par n² pour avoir une égalité avec des entiers et ... fais de l'arithmétique.

par **melreg** » 07 Fév 2008, 11:50

Le but est donc de voir que

.

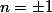
Si je suis ce que tu dis, je me retrouve avec:

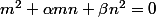
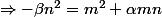
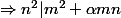
Mais n^2 ne divise pas m^2 (car m ne divise pas n)

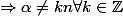
... autrement dit

n'est pas multiple de n...
Et puis?

par **yos** » 07 Fév 2008, 12:32

Non, la dernière étape est fausse

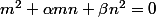
donc m^2=...
donc n|m^2, donc n=1 (ou -1).

par **melreg** » 07 Fév 2008, 13:18

Comme j'ai pu me retourner la tête... et c'est "juste" ça! Merci beaucoup de m'avoir mis sur la route!