Racine du polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ZIED0528
- Messages: 8
- Enregistré le: 07 Jan 2021, 14:07
-
 par ZIED0528 » 14 Jan 2021, 13:27
par ZIED0528 » 14 Jan 2021, 13:27
Soit le polynôme P donné par cette expression
=3z^{a+b+c}+e^{2\gamma}z^{a+b}+e^{2\beta}z^{a+c}+e^{2\alpha}z^{b+c}-e^{2(\beta+\gamma)}z^a-e^{2(\alpha+\gamma)}z^b-e^{2(\alpha+\beta)}z^c-3e^{2(\alpha+\beta+\gamma)},)
avec

et
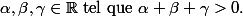
La question : quelles sont les conditions suffisantes sur les coefficient
s du polynôme P pour que ses racines soient en dehors du disque unité ??
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 14 Jan 2021, 18:24
par phyelec » 14 Jan 2021, 18:24
Bonjour,
vous pouvez peut-être appliquer le théorème d'Eneström-Kakeya qui dit :
soit
=\sum_{i=0}^{i=n} a_i z^i)
un polynôme à coefficients réels tels que
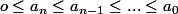
, alors les racines complexes sont en dehors du disque unité.
-
ZIED0528
- Messages: 8
- Enregistré le: 07 Jan 2021, 14:07
-
 par ZIED0528 » 16 Jan 2021, 00:47
par ZIED0528 » 16 Jan 2021, 00:47
Bonjour,
je peut pas utilisé le théorème d'Eneström-Kakeya parce que les coefficients du polynôme sont de signes différents.
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Jan 2021, 16:59
par phyelec » 16 Jan 2021, 16:59
Vous avez raison.
j'ai essayé de factoriser sans résultat.
La seule chose que j'ai remarquée est que si
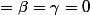
alors P(1)=0
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Jan 2021, 17:00
par phyelec » 16 Jan 2021, 17:00
lire
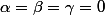
-
mathelot
 par mathelot » 16 Jan 2021, 17:18
par mathelot » 16 Jan 2021, 17:18
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Jan 2021, 17:36
par phyelec » 16 Jan 2021, 17:36
Oups, oubliez ce que j'ai écris c'est faux , sorry
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités