Bonjour,
j'aimerais savoir s'il est possible de trouver le déterminant d'une matrice grâce à sa racine carrée.
Racine carrée de matrice
4 messages
- Page 1 sur 1
Salut !
Posons ta matrice et
ta matrice et 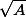 sa racine carrée.
sa racine carrée.
L'application) de
de ) dans
dans  est un morphisme du groupe
est un morphisme du groupe  , \times )) dans le groupe
dans le groupe  , \times)) i.e.
i.e. =\det(A) \times \det(B)) donc
donc 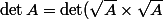 = \(\det(\sqrt A) \)^2) :+++:
:+++:
Scooby-doo a écrit:Bonjour,
j'aimerais savoir s'il est possible de trouver le déterminant d'une matrice grâce à sa racine carrée.
Posons
L'application
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Posonsta matrice et
sa racine carrée.
L'applicationde
dans
est un morphisme du groupe
dans le groupe
i.e.
donc
:+++:
Merci c'est plus clair !
Sais-tu comment je pourrais appliquer cela à une matrice quelconque (d'ordre nxn) dont les éléments peuvent prendre des valeurs de l'ensemble [1,99] pour trouver dans quels cas le det=0?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
