Racine carrée d'un matrice nilpotente

[alitshe]

Bonjour, alors voila je voudrais savoir s'il existe un théorème ou un "truc" évident sur la racine carrée d'une matrice nilpotente. Concrètement j'ai une matrice :

0010
0001
0000
0000

et je dois dire si elle admet une racine.
Cette matrice au carrée est égale à la matrice nulle.

[Nightmare]

Salut,

essaye la matrice avec que des 1 sur la diagonales supérieures. On sait bien comment calculer les puissances d'une matrice nilpotente généralement donc ce genre de résultat se conjecture assez facilement.

[alitshe]

Ha merci, en effet ca marche.

Est-ce qu'il y a une définition qui permet de savoir si la matrice nilpotente admet une racine? Car j'avoue que le feeling ne passe pas super bien entre les matrices et moi.

[Nightmare]

Il y a je crois une caractérisation avec les blocs de Jordan que j'ai vu dans un sujet d'agrég mais je ne m'en souviens plus.

Dans tous les cas à ton niveau tu peux rester au cas par cas, en espérant que les cas soient simples, ce qui est le cas ici.

[alitshe]

Oui je ne connais pas tout ca moi.
Je croise les doigts alors et je vais essayer d'en regarder quelques unes histoire dans "connaitre" un peu.

Merci beaucoup :)

[wserdx]

Je connais une caractérisation par les facteurs invariants (ce qui se ramène aux blocs de Jordan)
La matrice de départ a comme facteurs invariants , la racine carrée doit avoir des facteurs invariants qui sont aussi des puissances de . La seule possibilité, c'est 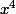, qui correspond à la matrice donnée par Nightmare.
Si ça vous tente, essayez de calculer la racine carrée de
0100
0000
0001
0000

(Il suffit de remarquer qu'elle a les mêmes facteurs invariants que la première et donc de calculer le changement de base qui permet de s'y ramener!)