Bonsoir, j'ai plusieurs questions, en vrac :
* A quelle condition peut-on faire un changement de variable dans une intégrale ?
* Peut-on montrer simplement (avec le programme de spé) qu'une matrice est toujours semblable à sa transposée ?
* Je crois qu'en fonction du K-ev E qu'on prend, il n'existe pas toujours de bases orthonormées pour une forme bilinéaire donnée de E*E dans K. Y'a-t-il une condition suffisante simple ?
* Si on prend une FBS phi, représentée dans la base B par la matrice A, est-il toujours vrai que phi(x,y)=transposée de x*A*y ? (Je pense que non...)
Quelqu'un peut-il m'éclairer svp ?
Questions en vrac
11 messages
- Page 1 sur 1
Salut,
Pour la question 1), à mon avis, c'est beaucoup trop vague comme question : parle tu d'intégralles aux sens de Riemann ?, de Stieltjes ?, de Lebesgue ? d'intégrales semi-convergentes ?
Cherche tu des conditions portant sur le changement de variable (la fonction phi telle que l'on "pose" x=phi(t)) ou plutôt sur la fonction f que l'on intègre ? etc...
Je n'ait absolument pas assez de "recul" pour te faire une réponse "globale" à toutes ces questions...
Pour la 2), ça marche avec la réduction en blocs de Jordan, mais cce n'est pas franchement "élémentaire"...
Pour la 3), je sais pas trop ce que tu attend comme réponse, mais, à part en caractéristique 2 (où là, il faut fortement revoir la copie), la méthode de "je sais plus qui" consistant à faire apparaitre des débuts d'identités remarquables a²+2ab+... dans l'écriture de la forme quadratique dans une base quelconque, ben ça marche tout le temps et il ne reste qu'à regarder si les facteurs constants qui apparaissent devant les carrés sont ou pas des carrés dans le corps considérés (ce qui dépend trés fortement du corps sur lequel on travaille).
Aprés, on peut aussi repérer dans la matrice associée en regardant la suite des déterminants kxk "en haut à gauche" de la matrice.
Pour la 4), à ton avis, c'est quoi la définition de "la matrice associée à une forme bilinéaire (pas forcément symétrique) dans une base B"?
Conclusion.
Pour la question 1), à mon avis, c'est beaucoup trop vague comme question : parle tu d'intégralles aux sens de Riemann ?, de Stieltjes ?, de Lebesgue ? d'intégrales semi-convergentes ?
Cherche tu des conditions portant sur le changement de variable (la fonction phi telle que l'on "pose" x=phi(t)) ou plutôt sur la fonction f que l'on intègre ? etc...
Je n'ait absolument pas assez de "recul" pour te faire une réponse "globale" à toutes ces questions...
Pour la 2), ça marche avec la réduction en blocs de Jordan, mais cce n'est pas franchement "élémentaire"...
Pour la 3), je sais pas trop ce que tu attend comme réponse, mais, à part en caractéristique 2 (où là, il faut fortement revoir la copie), la méthode de "je sais plus qui" consistant à faire apparaitre des débuts d'identités remarquables a²+2ab+... dans l'écriture de la forme quadratique dans une base quelconque, ben ça marche tout le temps et il ne reste qu'à regarder si les facteurs constants qui apparaissent devant les carrés sont ou pas des carrés dans le corps considérés (ce qui dépend trés fortement du corps sur lequel on travaille).
Aprés, on peut aussi repérer dans la matrice associée en regardant la suite des déterminants kxk "en haut à gauche" de la matrice.
Pour la 4), à ton avis, c'est quoi la définition de "la matrice associée à une forme bilinéaire (pas forcément symétrique) dans une base B"?
Conclusion.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
1) : Je parlais d'intégrales classiques, sur des segments finis et tout. Je voudrais savoir la condition pour qu'on puisse poser phi=..., je crois que ça doit être bijectif, mais de où à où ? Pouvez-vous m'aider svp ?
4) La définition de "la matrice associée à une forme bilinéaire (pas forcément symétrique) dans une base B", c'est la matrice des phi(e(i),e(j)) si B est la famille des e(i). Quand on écrit transposée de x*A*y, ça ne vaut phi(x,y) que si on écrit x et y dans B ?
4) La définition de "la matrice associée à une forme bilinéaire (pas forcément symétrique) dans une base B", c'est la matrice des phi(e(i),e(j)) si B est la famille des e(i). Quand on écrit transposée de x*A*y, ça ne vaut phi(x,y) que si on écrit x et y dans B ?
Pour ton 1) dans le cas des fonctions continues définies sur un intervalles fermé borné (cas dans lequel on a des primitives), cherche à retrouver (tout seul) quelle est la preuve du "théorème du changement de variable" (cela tient... une ligne) puis regarde si tu as utilisé quelque part le fait que le changement de variable est bijectif et tu aura ta réponse.
Indication : on peut parfaitement écrire le "théorème" sous la forme :
}^{\phi(b)}f(x)\,dx\ =\ \int_a^b f(\phi(t))\phi'(t)\,dt)
Ce qui montre qu'il est possible d'écrire le théorème sans utiliser la bijection réciproque de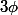 .
.
Bien entendu, je n'ais pas mis les hypothèses dans le "théorème" (ce qui n'est pas correct du tout) dans le but que... tu les retrouve.
Donc effectivement, si A c'est la matrice de phi dans une base B, il faut que (petit) x et (petit) y ce soit les matrices colonnes des coordonnées des vecteurs (grand) X et (grand) Y dans la même base B si on veut être sûr que phi(X,Y) (avec des grand X et Y) soit égal à txAy (avec des petit x et petit y)
Mais, cette "super constatation", ben c'est la même chose que de comprendre que faut pas multiplier une vitesse en m/s par des heures mais par des... secondes où alors il faut appliquer un "coeff multiplicateur" correspondant à un changement de base.
Indication : on peut parfaitement écrire le "théorème" sous la forme :
Ce qui montre qu'il est possible d'écrire le théorème sans utiliser la bijection réciproque de
Bien entendu, je n'ais pas mis les hypothèses dans le "théorème" (ce qui n'est pas correct du tout) dans le but que... tu les retrouve.
Bon, déjà, des formules d'algèbres linéaires qui continuent à marcher alors qu'on écrit pas tout les trucs dans la même base, ben forcément, il y en a pas beaucoup (sauf évidement si, dans la formule, il y a des matrices de changement de base...)aarnaud a écrit:Quand on écrit transposée de x*A*y, ça ne vaut phi(x,y) que si on écrit x et y dans B ?
Donc effectivement, si A c'est la matrice de phi dans une base B, il faut que (petit) x et (petit) y ce soit les matrices colonnes des coordonnées des vecteurs (grand) X et (grand) Y dans la même base B si on veut être sûr que phi(X,Y) (avec des grand X et Y) soit égal à txAy (avec des petit x et petit y)
Mais, cette "super constatation", ben c'est la même chose que de comprendre que faut pas multiplier une vitesse en m/s par des heures mais par des... secondes où alors il faut appliquer un "coeff multiplicateur" correspondant à un changement de base.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, car dans le cas "super gentil" où on a des primitives, ben le "théorème du changement de variable", c'est juste une réécriture de la formule qui dit que, si F et Phi sont dérivable sur ..., alors FoPhi l'est aussi et (FoPhi)'=F'oPhi.Phi'.aarnaud a écrit:Merci beaucoup. Pour le truc du changement de variable, il suffit que phi soit dérivable et f continue ?
Aprés, à mon avis, c'est pas forcément malin de ne donner que la version du théorème où on ne suppose pas Phi bijective.
Perso, je donne les deux versions aux étudiants car si on suppose f bijective, on peut écrire à gauche du = un truc qui ne contient pas la fonction Phi.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben, tout dépend ce que tu appelle "interessant"...
Perso, j'ai tendance à trouver que de savoir qu'elle est trigonalisable est trés interessant : si on doit faire des calculs "un peu bourrin", ça permet de ne les faire sur une matrice triangulaire, ce qui est beaucoup plus simple que sur une matrice quelconque.
Aprés, on peut dire "un peu mieux" que trigonalisable : on peut trouver une base dans laquelle la matrice est "sous forme de bloc de Jordan", c'est à dire une forme "assez proche" d'une forme diagonale.
Perso, j'ai tendance à trouver que de savoir qu'elle est trigonalisable est trés interessant : si on doit faire des calculs "un peu bourrin", ça permet de ne les faire sur une matrice triangulaire, ce qui est beaucoup plus simple que sur une matrice quelconque.
Aprés, on peut dire "un peu mieux" que trigonalisable : on peut trouver une base dans laquelle la matrice est "sous forme de bloc de Jordan", c'est à dire une forme "assez proche" d'une forme diagonale.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Quand je disais "intéressant", je pensais à l'endomorphisme. On peut pas poser v(x+iy)=u(x)+iu(y) (où x et y sont dans R^n), puis dire que la matrice de v c'est celle de u... enfin je ne sais pas si ça mène quelque part, mais comment se traduit le fait que la matrice d'un endomorphisme de R^n est trigonalisable dans C ?
Ben, c'est pas trop compliqué car, si ta matrice est à coeff. réel alors son polynôme caractéristique l'est aussi donc les éventuelles valeurs propres complexes sont deux à deux conjugués et tu peut prendre comme vecteurs propres pour l'une des valeur propre les conjugués des vecteurs propres de l'autre et cela donne une "forme" plus ou moins canonique dans laquelle on peut mettre la matrice de départ.
Par exemple, si dans C la matrice est diagonalisable, le "bloc conjugué") dans C devient naturellement le bloc
dans C devient naturellement le bloc ) dans R où
dans R où 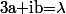
Dans le cas trigonalisable, c'est un peu plus lourd, mais il y a le même type de "conversion".
C'est en fait à peu prés le même type de "conversion" que dans le cas des équa-diff linéaires à coeff constant où on passe des solutions à valeurs complexes (en t^?.exp(lambda.t) avec lambda complexe) aux solutions réelles (en t^?.cos(a.t).exp(b.t) avec a,b réels)
Par exemple, si dans C la matrice est diagonalisable, le "bloc conjugué"
Dans le cas trigonalisable, c'est un peu plus lourd, mais il y a le même type de "conversion".
C'est en fait à peu prés le même type de "conversion" que dans le cas des équa-diff linéaires à coeff constant où on passe des solutions à valeurs complexes (en t^?.exp(lambda.t) avec lambda complexe) aux solutions réelles (en t^?.cos(a.t).exp(b.t) avec a,b réels)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
