Bonjour,
1) Pourquoi parle-t-on de famille de vecteurs et pas plutôt de suite de vecteurs?
2) J'ai lu qu'une famille était une application de I un ensemble d'indices dans E un ensemble quelconque.
Or je vois également une autre définition, par exemple pour une famille finie de p vecteurs de E : "Une famille finie de p vecteurs de E est un p-uplet (u1,...,up) de vecteurs de E."
Et là je ne vois pas le lien avec la première définition: un p-uplet ce n'est pas la même chose qu'une application!
Merci d'avance,
PLB
Questions sur les familles
6 messages
- Page 1 sur 1
Re: Questions sur les familles
Bonjour
Pour la premièr question : une suite est plutôt une application de dans un ensemble E, ou plus généralement d'une section finissante de
dans un ensemble E, ou plus généralement d'une section finissante de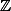 (c-à-d
(c-à-d  ) dans un ensemble E
) dans un ensemble E
Donc c'est une liste infinie.
Une famille n'est pas forcément infinie.
Lorsqu'elle est indicée par un ensemble d'indices I, c'est donc bien une application de I dans E.
Enfin, vous avez raison un p-uplet n'est pas une application, mais il est facile de faire une bijection entre (l'ensemble des applications de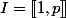 dans E) et
dans E) et 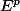
Pour la premièr question : une suite est plutôt une application de
Donc c'est une liste infinie.
Une famille n'est pas forcément infinie.
Lorsqu'elle est indicée par un ensemble d'indices I, c'est donc bien une application de I dans E.
Enfin, vous avez raison un p-uplet n'est pas une application, mais il est facile de faire une bijection entre (l'ensemble des applications de
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Questions sur les familles
D'accord je vois, donc la définition avec les p-uplets est équivalente?
Re: Questions sur les familles
Hello,
tu peux avoir une famille (infinie) indicée par un paramètre réel, par exemple x->exp(a*x), où a varie dans R
tu peux avoir une famille (infinie) indicée par un paramètre réel, par exemple x->exp(a*x), où a varie dans R
Re: Questions sur les familles
bonjour,
dans le cas de famille indexée par un ensemble I, I est tout à fait quelconque et notamment n,'a pas besoin d'être ordonné.
dans le cas de famille indexée par un ensemble I, I est tout à fait quelconque et notamment n,'a pas besoin d'être ordonné.
Re: Questions sur les familles
pierrelouisbourgeois a écrit:D'accord je vois, donc la définition avec les p-uplets est équivalente?
en l'occurrence oui, car un ensemble fini d'indices peut toujours être ordonné.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
