Questions sur la combinatoire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 16 Déc 2010, 13:09
Bonjour,
j'ai plusieurs questions de combinatoire , que je n'arrive pas trop a résoudre ,
D'abord , comment montrer que
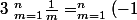^{m+1}\frac{C_n^m}{m})
De même comment montrer que
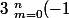^mC_n^mC_{p+m}^n=(-1)^n)
Je suis a peu près certain que la deuxième provient d'un produit de développement de puissances issues du binôme de Newton, mais je ne vois pas du quel .. pour la première je suis un peu sec, la récurrence ne marche pas .. alors je vois pas trop ..
Merci de votre aide !
[/TEX]
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
par Euler07 » 16 Déc 2010, 13:25
Salut Benekire, as tu testé les premières valeur pour voir comment cela évolue
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
par Euler07 » 16 Déc 2010, 13:31
Tu le fais par récurrence
:zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 16 Déc 2010, 13:38
Ah oui , mince , j'avais zapé de séparer mon coefficient binomial :mur: Merci Euler !!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 17 Déc 2010, 09:53
Quelqu'un a une idée pour la deuxième ? Merci !
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 17 Déc 2010, 14:16
Salut,
Déjà, pour donner une autre preuve pour le 1), perso, dés que je vois
^{k+1}}{k}{k\choose n})
, j'écrit sans réfléchir que
)
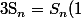où
=\Bigsum_{k=1}^{n}\frac{(-1)^{k+1}}{k}{k\choose n}x^k)
(ce qui, en intégrant/dérivant me permet de faire apparaitre/disparaitre des termes)
=\Bigsum_{k=1}^{n}{k\choose n}(-x)^{k-1}<br />=\ \frac{\ \ 1}{-x}\,\Big(-1+\Bigsum_{k=0}^{n}{k\choose n}(-x)^k\Big)=\frac{1-(1-x)^n}{x})
donc
=S_n(1)-S_n(0)=\int_0^1S'_n(x)\,dx=\int_0^1\frac{1-(1-x)^n}{x}\,dx<br />=\int_0^1\frac{1-t^n}{1-t}\,dt<br />=\int_0^1(1+t+t^2+...+t^{n-1})dt<br />=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})
Pour le 2), le truc pas con à savoir, c'est que :
- Les LIGNES du triangle de pascal correspondent (évidement) à
^l=\Bigsum_{c=0}^{l}{l\choose c}X^c)
- Mais les COLONNES du triangle de pascal correspondent à
^{-c-1}=\Bigsum_{l=c}^{\infty}{l\choose c}X^{l-c})
Donc
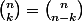
est le coeff. en
dans
^n)
Et
^{p+k-n}{p+k\choose n})
est le coeff. en
dans
^{-n-1})
.
D'où, si
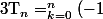^{k}{n\choose k}{p+k\choose n})
, alors
^{p-n}T_n=\Bigsum_{k=0}^{n}(-1)^{p+k-n}{n\choose k}{p+k\choose n})
est le coeff. en
dans
^n\times(1+X)^{-n-1}=(1+X)^{-1}=\Bigsum_{k=0}^{\infty}(-1)^{k}X^k)
.
On en déduit que
^{p-n}T_n=(-1)^p)
, c'est à dire que
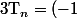^n)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 17 Déc 2010, 14:27
Merci Ben !
La méthode du 1 est très intéressante , et pour le deux je me doutais fort que ça venait d'un produit mais ... j'ignorais lequel ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 17 Déc 2010, 15:20
Ben314 a écrit:- Mais les COLONNES du triangle de pascal correspondent à
Je reviens sur ce point , comment tu fais pour obtenir ça ? J'ai jamais entendu parler des colonnes du triangle de pascal ... Et puis tu est sûr que l'exposant de X est pas plutôt c-l ?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 17 Déc 2010, 15:48
Oui, je suis sûr que c'est bien L-C.
En fait tu peut voir cette formule
- Soit comme un développement FORMEL, c'est à dire où X ne désigne absolument rien et cela signifie que, si on développe formellement (1-X)^{c+1} fois la série alors on obtient 1.
- Soit comme un développement en série d'une fonction de la variable réelle (ou complexe) X et dans ce cas il faut préciser que le développement est valable pour |X|<1.
Une des façons les plus élémentaires d'obtenir le résultat est de partir de (1-X)^{-1}=1+X+X²+X³+... et de dériver C fois cette relation.
Si tu raisonne en terme de fonction et pas formellement (ce qui me semble préférable quand on sait pas trop ce qu'est une série formelle...) il faut vérifier que l'on a le droit de dériver cette somme infinie, mais c'est assez simple en considérant uniquement la somme des x^k de k=0 à n et en majorant l'erreur commise...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
par benekire2 » 17 Déc 2010, 15:52
Oui , je sais pas trop ce qu'est une série "formelle" alors je vais faire avec la deuxième méthode , je regarde tout ça, merci bien !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
