Question sur le programme Mathematica

par **Cherrys** » 10 Déc 2008, 10:34

Bonjour

J'ai utilisé le programme mathématica pour simuler la projection stéréographique de la fibration de hopf. J'aimerais modifier un petit truc au rendu graphique de la simulation, mais ne maitrise pas du tout ce programme...

Voila donc mon image est comme ca: http://img244.imageshack.us/my.php?image=simulationjv3.png
Elle est paramètrisée à l'aide de la commande ParametricPlot3D, et j'ai 2 paramètres. Sur l'image, on voit des cercles, certains en "diagonale" par rapport aux sortes de tores sur lesquels ils sont, d'autres perpendiculaires a un axe (celui qui va de gauche a droite). Ces cercles correspondent en quelque sortes a des lignes de coordonnée par rapport a mes paramètres. Bref ce que j'aimerais faire, c'est n'afficher que les cercle correspondant à l'un des paramètres (ceux en diagonale), mais pas les autres, afin d'optenir un image un peu comme celle ci: http://www-fourier.ujf-grenoble.fr/~bkloeckn/images/Hopf.jpg

Est-ce que l'un d'entre vous aurait une idée de comment faire ca? Merci d'avance!

par **busard_des_roseaux** » 10 Déc 2008, 11:08

Bjr,

effectivement, les cercles dont tu parles ont l'air "triviaux"
sur wiki, la projection liée à la fibration de Hopf est donnée analytiquement par

avec

peut être voir d'où vient la seconde coordonnée constante dans l'espace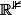

d'arrivée de la projection pour réduire le domaine de départ sur

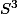. Les cercles triviaux sont en effet
d'ordonnée constante.

par **Cherrys** » 10 Déc 2008, 11:41

mon problème ne vient pas du choix de la paramètrisation, mais uniquement d'une option de mathematica. J'ai besoin de 2 paramètres pour simuler chacun de mes sortes de tores, mais l'un des paramètre paramètrise une fibre au dessus d'un point donné, l'autre paramètrise l'ensemble des points dont on veut représenter la fibration, et donc tourne simplement autours du tore, donnant ces cercles triviaux.
Je cherche donc une option du genre Ligne de coordonnée->[true,false] que je met a la fin du code dans mathematica, afin de n'afficher qu'une seul des 2 ligne de coordonnée.
Je ne sais pas si c'est possible, mais étant donné que ce programme est très complet, j'espère que ca l'est^^

par **nuage** » 10 Déc 2008, 15:25

Salut,
utilise la directive graphique

Code: Tout sélectionner: EdgeForm[ ]

avec rien entre les crochets pour supprimer les lignes automatiques puis trace les lignes que tu veux voir.
Dans la mesure où les lignes tracées automatiquement sont les bord des polygones je ne crois pas que l'on puisse faire mieux, mais je suis resté à mathemetica 2.0 ... alors RTFM

par **Cherrys** » 10 Déc 2008, 19:01

nuage a écrit:Salut,
utilise la directive graphique
Code: Tout sélectionner
EdgeForm[ ]
avec rien entre les crochets pour supprimer les lignes automatiques puis trace les lignes que tu veux voir.
Dans la mesure où les lignes tracées automatiquement sont les bord des polygones je ne crois pas que l'on puisse faire mieux, mais je suis resté à mathemetica 2.0 ... alors RTFM

Etant donné que les lignes que je veux voir sont un ensembles d'une soixantaine de cercles de Villarceau (4 tores avec une quinzaine de cercles sur chacun d'entre eux), je me vois mal dessiner ça à la main... Mais je vais quand meme essayer de faire quelque chose avec cette commande.

Pour le RTFM, le programme est sur les ordinateur de l'université dans laquelle j'étudie, donc je n'ai pas de manuel. Et si je n'ai rien trouvé qui corresponde à mon problème en cherchant sur internet... Mais j'avais cru comprendre que les forums étaient là pour partager nos expériences, et donc je demande au cas ou quelqu'un se serait retrouvé avec une problème similaire, et aurait trouvé une solution. >_>

par **nuage** » 10 Déc 2008, 20:45

J'ai le sentiment que tu as mal pris mon message. :briques:
je ne voulais pas (trop) te critiquer.
Pour dessiner les cercles de Villarceau tu reprends ton paramétrage et au lieu de dessiner une surface tu demande des lignes.
Disons que si le paramètre qui dessine les cercles triviaux est

et que l'autre est

tu écris qqc du genre

Code: Tout sélectionner: lignes=Table[ Line[ Table[{x(u,v),y(u,v)},{v,..,..}]],{u,..,..}]

Puis tu utilises

Code: Tout sélectionner: Show[{graphiquesansligne,Graphics3D[lignes]}];

En tout cas je l'ai fait et ça marche.
Si tu veux faire plus beau tu peut remplacer les lignes par des tores assez fins, mais l'écriture commence à devenir lourde.

Pour faire vraiment bien, dans le genre de ton deuxième lien, tu peux utiliser PovRay. Mais là il faut faire la plus part des calculs à l'extérieur du programme.

Quand au manuel : il y a une aide dans le programme me semble-t-il.
Et si je t'ai répondu c'est bien parce qu'il n'est pas évident de trouver des choses du genre EdgeForm, pour le reste il n'est pas inutile de la consulter.

A+

par **Cherrys** » 10 Déc 2008, 23:33

ok merci beaucoup, je vais essayer ca :)

par **Cherrys** » 11 Déc 2008, 12:49

Bon ca marche pas... Si j'essaie d'ajouter EdgeForm[], y'as tout qui plante...

Si ca peut aider a faire avancer le shmilblick, voila mon code:

Code: Tout sélectionner: z = 0.1 y = 0.6 x = -0.8 a = 0.999999 ParametricPlot3D[{{(Sqrt[ 1/(2*(z + 1))]/(1 + Sqrt[(z + 1)/2]*Sin[t]))*(Cos[ t]*(z + 1)), (Sqrt[ 1/(2*(z + 1))]/(1 + Sqrt[(z + 1)/2]*Sin[t]))*(Cos[t]*Cos[u] + Sin[t]*Sin[u]), (Sqrt[ 1/(2*(z + 1))]/(1 + Sqrt[(z + 1)/2]*Sin[t]))*(Cos[t]*Sin[u] - Sin[t]*Cos[u])}, {(Sqrt[ 1/(2*(y + 1))]/(1 + Sqrt[(y + 1)/2]*Sin[t]))*(Cos[ t]*(y + 1)), (Sqrt[ 1/(2*(y + 1))]/(1 + Sqrt[(y + 1)/2]*Sin[t]))*(Cos[t]*Cos[u] + Sin[t]*Sin[u]), (Sqrt[ 1/(2*(y + 1))]/(1 + Sqrt[(y + 1)/2]*Sin[t]))*(Cos[t]*Sin[u] - Sin[t]*Cos[u])}, {(Sqrt[ 1/(2*(x + 1))]/(1 + Sqrt[(x + 1)/2]*Sin[t]))*(Cos[ t]*(x + 1)), (Sqrt[ 1/(2*(x + 1))]/(1 + Sqrt[(x + 1)/2]*Sin[t]))*(Cos[t]*Cos[u] + Sin[t]*Sin[u]), (Sqrt[ 1/(2*(x + 1))]/(1 + Sqrt[(x + 1)/2]*Sin[t]))*(Cos[t]*Sin[u] - Sin[t]*Cos[u])}, {(Sqrt[ 1/(2*(a + 1))]/(1 + Sqrt[(a + 1)/2]*Sin[t]))*(Cos[ t]*(a + 1)), (Sqrt[ 1/(2*(a + 1))]/(1 + Sqrt[(a + 1)/2]*Sin[t]))*(Cos[t]*Cos[u] + Sin[t]*Sin[u]), (Sqrt[ 1/(2*(a + 1))]/(1 + Sqrt[(a + 1)/2]*Sin[t]))*(Cos[t]*Sin[u] - Sin[t]*Cos[u])}}, {u, 0, 2 Pi}, {t, 0, 2 Pi}, PlotStyle -> Opacity[0.5], PlotRange -> {{ -6, 6}, { -6, 6}, {-6 , 6}}]

J'ai essayé de mettre le EdgeForm après les 3 coordonnée de chacune de mes surfaces, ou après toute les paramètrisations de surface, ou au meme niveau du les autres options de graphique, rien a faire... soit ca me fait des graphs ne voulant plus rien dire, soit j'ai eu une fois un graphe tout noir, ou encors le programme freez et je suis obligé de forcer sa fermeture... Bref je capte pas comment faire

par **nuage** » 11 Déc 2008, 18:30

Salut,
une méthode : si graligne est le nom de ton graphique cad tu ajoutes

Code: Tout sélectionner: graligne = ParametricPlot3D[...

ensuite

Code: Tout sélectionner: Show[Graphics3D[{EdgeForm[], graligne[[1]],ligne}]]

et normalement ça marche.

par **Cherrys** » 16 Déc 2008, 13:43

bon bein ca marche pas, ca me donne un cercle en 2 dimentions avec des lignes radiales... Mais bon, c'est pas grave, j'ai changé l'angle de vue, et ca me donne quelque chose d'assez joli, donc tant pis s'il y a des lignes en trop :)

Question sur le programme Mathematica

Question sur le programme Mathematica

Qui est en ligne