Question sur "mesure et integration "

par **ClaireD** » 22 Sep 2007, 14:36

Bonjour,
je suis étudiante en 3ème année de maths et je me pose une question :

soit f une fonction bornée sur [a,b].
soit E l'ensemble de ses points de discontinuités.

w(f,x)= inf { sup(f(y)) - inf(f(y)), |x-y|0) (y dans [a,b] )

on appelle w(f,x) l'oscillation de f en x dans [a,b]

on veut montrer que pour §>0 E§ = { x tel que w(f,x) >= § } est un fermé.

j'avais pensé à utiliser le théorème : "toute image reciproque d'un fermé par une fonction continue f est un fermé"
Seulement je n'arrive pas à montrer que w est continue...c'est cela qui me gène...c'est surement tout bete.... :hum: je dois trop me compliquer :mur:
Si vous avez des suggestions n'hesitez pas :happy2:
Merci,
Claire.

par **aviateurpilot** » 22 Sep 2007, 14:41

cette ecriture (inf { sup(f(y)) - inf(f(y)), |x-y|<delta }) n'a pas de sens !!!
faut dire dire sup(f(y)) quand y parcour [???]
si tu veux dire sup(f(y))

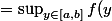et inf(f(y))

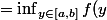dans ce cas la condition |x-y|<delta signifie koi???

par **legeniedesalpages** » 22 Sep 2007, 14:48

l'oscillation de f est au point a est défini par

.

Donc j'interpréterais plutôt comme ça:

par **ClaireD** » 22 Sep 2007, 15:21

aviateurpilot a écrit:cette ecriture (inf { sup(f(y)) - inf(f(y)), |x-y|<delta }) n'a pas de sens !!!
faut dire dire sup(f(y)) quand y parcour [???]
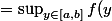si tu veux dire sup(f(y)) et inf(f(y))
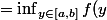dans ce cas la condition |x-y|<delta signifie koi???

je sais bien que ça n'a pas de sens mais je suis nouvelle sur ce firum donc désolée j'ai un peu de mal à écrire correctement les formules de maths...

par **ClaireD** » 22 Sep 2007, 15:22

legeniedesalpages a écrit:l'oscillation de f est au point a est défini par .

Donc j'interpréterais plutôt comme ça:

ouii c'est exactement ça.

Question sur "mesure et integration "

question sur "mesure et integration "

Qui est en ligne