Salut !
Oui, c'est vrai. Si tu as

vecteurs linéairement indépendant
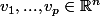
, avec
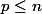
, alors l'espace vectoriel
)
est un sous-espace vectoriel de dimension
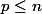
.
Si tu considère
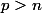
vecteurs linéairement indépendant de

, tu vas pouvoir engendrer avec un espace vectoriel de dimension
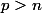
, ce qui est impossible dans

.
Exemple : Dans

, un vecteur non nul est toujours linéairement indépendant et engendre un sous-espace vectoriel de dimension 1 : c'est une droite passant par (0,0,0).
Si tu prends deux vecteurs non nuls linéairement indépendant alors ils engendrent un espace vectoriel de dimension 2 : c'est un plan passant par (0,0,0).
Si tu prends trois vecteurs non nuls linéairement indépendant alors ils engendrent un espace vectoriel de dimension 3 : c'est un l'espace tout entier.
Si tu prends quatre vecteurs non nuls linéairement indépendant alors ils engendrent un espace vectoriel de dimension 4 : c'est impossible d'avoir un sous-espace vectoriel de dimension 4 dans un espace vectoriel de dimension 3 !
De manière générale, quel que soit la famille libre

et la famille génératrice

de ton espace vectoriel

de dimension finie, on a toujours
 \le \dim(E) \le {\rm card}(G))
.
