est ce que on peut ecrire ce ci
(-1)^1= (-1)^(3/3)
Question simple
12 messages
- Page 1 sur 1
eriadrim a écrit:Je dirais que sinon de la même façon, on pourrait dire que 1 = 2/2 et donc :
Du coup, je pense que c'est à cause de ce genre d'ambiguïté que l'on ne peut pas dire que c'est correct
Salut, il y avait déjà eu un sujet de ce type... En fait ça dépend dans quel ensemble tu te places.
Eriadrim quand tu écris
Bref dans tous les cas t'es sauvé par les conventions mais pour pimenter un peu les choses on pourrait se demander ce qu'il en est de
eriadrim a écrit:Je dirais que sinon de la même façon, on pourrait dire que 1 = 2/2 et donc :
Je crois que c'est différent. Quand on a [TEX]((-1)^2)^{1/2}[TEX] on doit pouvoir intervertir la position de 1/2 et 2 en puissance. Or, cela n'est pas possible tant qu'on est dans R, car la fonction racine carré est définie sur R+, donc -1 est exclu.
Ainsi, je pense que c'est à cause de l'exclusion de -1, que tu as obtenu ce résultat "absurde". Donc la comparaison n'est pas valable.
Bonjour.
En toute rigueur on n'a pas l'égalité ensembliste mais 1 et \dfrac{a}{a} sont identifiés via une bijection et une relation d'équivalence (Rappelles-toi et rappelez-vous les constructions de \mathbb{Z} et \mathbb{Q}). Ces problèmes d'égalité et d'identification ressurgissent parfois. Il ne faut pas confondre les fonctions polynomiales avec les fonctions puissance. C'est pour éviter ce genre de problème qu'on ne définit les fonctions puissances
mais 1 et \dfrac{a}{a} sont identifiés via une bijection et une relation d'équivalence (Rappelles-toi et rappelez-vous les constructions de \mathbb{Z} et \mathbb{Q}). Ces problèmes d'égalité et d'identification ressurgissent parfois. Il ne faut pas confondre les fonctions polynomiales avec les fonctions puissance. C'est pour éviter ce genre de problème qu'on ne définit les fonctions puissances 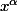 que pour
que pour 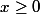 si
si  et que pour
et que pour  ici
ici  (Des abus de notation, j'en ai faits). On montre ensuite que cette définition ne dépend du représentant de
(Des abus de notation, j'en ai faits). On montre ensuite que cette définition ne dépend du représentant de  choisi
choisi
MOHAMED_AIT_LH a écrit:En fait je me suis basé sur l fait que chbicheb pose la question siuniquement quand
et
.
Si ce n'est pas le cas , je retire ma remarque ci-dessus.
En toute rigueur on n'a pas l'égalité ensembliste
Bonjour.
En toute rigueur on n'a pas l'égalité ensembliste pour
pour  mais 1 et
mais 1 et  sont identifiés via une bijection et une relation d'équivalence (Rappelles-toi et rappelez-vous les constructions de
sont identifiés via une bijection et une relation d'équivalence (Rappelles-toi et rappelez-vous les constructions de  et
et  ). Ces problèmes d'égalité et d'identification ressurgissent parfois. Il ne faut pas aussi confondre les fonctions polynomiales avec les fonctions puissance. C'est pour éviter ce genre de problème qu'on ne définit les fonctions puissances
). Ces problèmes d'égalité et d'identification ressurgissent parfois. Il ne faut pas aussi confondre les fonctions polynomiales avec les fonctions puissance. C'est pour éviter ce genre de problème qu'on ne définit les fonctions puissances 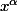 que pour
que pour 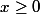 si
si 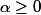 et que pour
et que pour  si
si 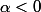 (Des abus de notation, j'en ai faits). On montre ensuite que cette définition ne dépend du représentant de
(Des abus de notation, j'en ai faits). On montre ensuite que cette définition ne dépend du représentant de  choisi.
choisi.
L'écriture^{ab}=((-1)^a)^b) n'est valable que pour
n'est valable que pour  et
et  entiers naturels puisque le sens qu'on peut donner à
entiers naturels puisque le sens qu'on peut donner à ^{ab}) est celui des fonctions polynomiales et non pas fonctions puissances.
est celui des fonctions polynomiales et non pas fonctions puissances.
En toute rigueur, la réponse est non car^{(3/3)}) n'est pas défini
n'est pas défini
MOHAMED_AIT_LH a écrit:En fait je me suis basé sur l fait que chbicheb pose la question siuniquement quand
et
.
Si ce n'est pas le cas , je retire ma remarque ci-dessus.
En toute rigueur on n'a pas l'égalité ensembliste
L'écriture
En toute rigueur, la réponse est non car
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
