Question de signe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 18:34
par kokorico06 » 03 Nov 2011, 18:34
Juste un petit souci de signe que je ne comprend pas !
je dois résoudre l'équation arcsinx = arccos(1/3) - arccos(1/4)
après quelques manip' je trouve x = +/- (rac(15) - rac(8))/12
Sauf que dans la correction, ils ne gardent que la solution négative! Je ne comprend pas réellement pourquoi.
Je pense qu'il faut avant toute chose que je regarde le signe de arccos(1/3) - arccos(1/4)
Mais je ne sais pas comment faire.
Merci pour votre aide par avance !
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 03 Nov 2011, 19:11
par Dlzlogic » 03 Nov 2011, 19:11
Bonsoir, je pense que pour vous aider à comprendre, il faudrait voir la correction.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 19:19
par Skullkid » 03 Nov 2011, 19:19
kokorico06 a écrit:Je pense qu'il faut avant toute chose que je regarde le signe de arccos(1/3) - arccos(1/4)
Bonjour, tu penses bien. Quel est le sens de variation de arccos ?
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:19
par kokorico06 » 03 Nov 2011, 19:19
Lol c'est ce que j'ai fait mais la correction c'est juste la réponse ! Pas d'explications supplémentaires ^^
Ce sont des exos sur internet !
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:33
par kokorico06 » 03 Nov 2011, 19:33
arccosx est décroissante sur ]-1;1[ et sur ]1; +infini[
donc arccos(1/3) - arccos(1/4) est négatif
et c'est pour ça qu'on prend la valeur négative de x ?
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:37
par kokorico06 » 03 Nov 2011, 19:37
Heu décroissante sur ]-1;1[ plutôt !
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 19:39
par Skullkid » 03 Nov 2011, 19:39
Oui (enfin plutôt [-1,1] pour être plus large), arccos(1/3) - arccos(1/4) est négatif, donc si x est solution, arcsin(x) est négatif, et donc...
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:43
par kokorico06 » 03 Nov 2011, 19:43
Oui mais arcsin x est positif pour tout x dans ]-1;1[
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:46
par kokorico06 » 03 Nov 2011, 19:46
Ah oui oui c'est bon ! arcsin n'est pas positif sur ]-1;1[ mais sur [0;1[, j'ai un peu confondu la sifne de la dérivée et le signe de la fonction elle même ^^ Je suis surement fatiguée :)
Merci en tout cas ! Bonne soirée
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 19:47
par Skullkid » 03 Nov 2011, 19:47
kokorico06 a écrit:Oui mais arcsin x est positif pour tout x dans ]-1;1[
Combien vaut arcsin(-1) ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 19:48
par Skullkid » 03 Nov 2011, 19:48
Oui, et arcsin est définie sur [-1,1], pas uniquement sur ]-1,1[ (elle n'est dérivable que sur ]-1,1[ en revanche).
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 19:52
par kokorico06 » 03 Nov 2011, 19:52
Ah oui effectivement :)
-
mathelot
 par mathelot » 04 Nov 2011, 07:59
par mathelot » 04 Nov 2011, 07:59
kokorico06 a écrit:arccosx est décroissante sur ]-1;1[ et sur ]1; +infini[
arccos x veut dire : "longueur d'arc dont le cosinus est x"
c'est peu probable que

tout est expliqué
ici
-
mathelot
 par mathelot » 04 Nov 2011, 08:23
par mathelot » 04 Nov 2011, 08:23
c'est bizarroïde, je trouve naturellement
au plus une solution ?
on remarque que
>0)
en prenant le sinus des deux membres de l'équation
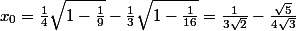
 \in ]\frac{\pi}{3},\frac{\pi}{2}[)
car arccos() est décroissante
 \in ]\frac{\pi}{3},\frac{\pi}{2}[)
 -arccos (\frac{1}{4}) < 0)
donc la solution négative

convient
-
mathelot
 par mathelot » 04 Nov 2011, 08:40
par mathelot » 04 Nov 2011, 08:40
.....................................................................................
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
