Question series de taylors

[Veelox]

Bonjour, jai une question ou il me demande de trouver le plus petit degree du polynome de taylor necessaire pour evaluer lintegral de sin (t)/t de 0 a 1 avec.une erreur plus petite que 10^(-10). Je suis complètement . bloquer je trouve rien sur internet. Merci de meclairer:)

[Veelox]

Il y a aussi une question qui est : soit T (x) la series de taylor dune fonction f (x) autour de a. Supposons que cette series possede un rayon de convergence R. Trouver lintervalle de valeur.y dans lequel la series de taylor de f (y^(2)) converge. Justifier.votrr reponse. Encore une fois je trouve rien

[Mimosa]

Bonjour

1) C'est un résultat général sur les séries. Si la série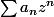 converge pour 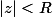la série 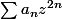converge certainement pour 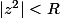c'est-à-dire pour .

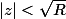2) Ecris la série à intégrer, intègre là et majore le reste.

[Veelox]

Bonjour

1) C'est un résultat général sur les séries. Si la série converge pour la série converge certainement pour c'est-à-dire pour .

2) Ecris la série à intégrer, intègre là et majore le reste.

Merci beaucoup de votre aide. Pour le 2) jai reussi a integrer la series. Jai par la suite developper jusqua des nombre de l'ordre de 10 E -11, par contre je ne sais juste pas comment je devrais terminer.
Par la suite pour votre 1) je ne comprend toujours pas :$. Je sais que f (x) converge si x element ]a-r ; a+r[. Sa veux dire que si x=y^2, y est élément de ]a-sqrt (R) ; a+ sqrt (R) [ ??? Sqrt etant squareroot

[Mimosa]

Oui, c'est ça pour la une. Pour finir la deux, il faut résoudre l'inéquation

[Mimosa]

Mais j'ai répondu!