Question large : Polynômes de Tchebychev

[David R.]

Bonjour à vous, communauté exceptionnelle,

Depuis quelques temps, je m'intéresse aux frises algébriques (frieze patterns, définies par Conway et Coxeter : http://www.link.cs.cmu.edu/15859-s11/notes/frieze-patterns-gazette.pdf). Ce concept est intimement lié à la notion de polynômes continuants signés, aussi appelés polynômes de Tchebychev généralisés. Comme ce second nom l'indique ceux-ci sont définis analogiquement aux polynômes de Tchebychev. C'est dans cette optique que je m'intéresse à la motivation derrière ces polynômes.

J'ai lu plusieurs articles sur Internet qui expliquent en long et en large comment obtenir le n-ième polynôme de Tchebychev à partir de la formule de récurrence, ainsi que les propriétés qui y sont associées, mais, généralement, les articles ne sont pas plus profonds. J'en ai trouvé d'autres qui, au contraire, étaient trop compliqués pour moi et mon cerveau sous-développé, m'empêchant d'approfondir mes connaissances sur le sujet.

J'ai compris que le n-ième polynôme de Tchebychev est tel qu'il admet exactement n racines, situées uniformément dans l'intervalle [0,1]. J'ai aussi lu qu'il s'agissait des "monic polynomials" (je ne suis pas certain de la traduction française) dont la valeur maximale (en valeur absolue) de la fonction dans l'intervalle [0,1] est minimale. Je n'ai toutefois pas trouvé de preuve satisfaisante à cet énoncé. D'ailleurs, s'agit-il des uniques "monic polynomials" tels? Finalement, j'ai aussi lu que ces polynômes avaient des utilités dans l'interpolation polynomiale, mais je n'ai pas vraiment compris pourquoi, ni comment.

Donc voilà, si quelqu'un a un lien vers un article simple et détaillé ou si quelqu'un connaît bien ces polynômes et peut m'expliquer le mieux possible la motivation derrière ces polynômes, ainsi que leurs applications concrètes, j'en serais énormément reconnaissant! =)

Merci d'avance,
David

[Le_chat]

Salut.

Les polynômes de Tchebychev sont une suite de polynômes, telle que le n e polynôme vérifie Tn(cos(t))=cos(nt) pour tout t dans R. On peut montrer très facilement qu'une telle suite de polynômes existe et est unique, que Tn est de degré n et de coefficient dominant 2^n.

Par exemple, cos(2t)=2cos^2(t)-1, on en tire T2=2*X^2-1.
Pour les racines, on sait que cos(nt)=0 pour t=(2k-1)pi/2n, k allant de 1 à n. On en tire que les cos((2k-1)pi/2n) sont racines de Tn, et comme elles sont n est distinctes, on a toutes les racines de Tn, et on remarque qu'elles sont réparties dans [-1,1] ( pas dans [0,1]).

Concernant le "monic polynomial", cela dit précisément que si on prend P un polynôme de degré n, qui est unitaire, la plus grande valeur prise par |P| sur [-1,1] est plus grande que 2^-n, et que cette valeur est 2^-n si et seulement si P est plus ou moins Tn/2^n. On divise par 2^n pour obtenir un polynôme unitaire (le coefficient dominant de Tn est 2^n).

En ce sens, ce sont les seuls "monic polynomial". Pour une preuve il y a ça: http://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/Polynomes/CCP_2003_MP_M1_Enonce.pdf, c'est la partie 3 qui en parle.

Pour l'approximation polynomiale, je ne sais pas trop comment ça marche, mais ils doivent être pratique car en un sens ce sont les polynômes de degré n qui restent "le plus près"de 0 sur l'intervalle [-1,1].

Je ne connais pas grand chose d'autre là dessus, mais j'espère que ça te sera utile.

[David R.]

Merci beaucoup pour cette réponse rapide. Je vais lire en profondeur ce soir (heure du Québec) et te reviens là-dessus! =)

[sinusx]

Salut,

Si tu cherches des applications de ces polynômes, il y a beaucoup de choses dans le cours de A. Magnus (Ch 2)...

[David R.]

Donc, d'abord, merci beaucoup pour vos réponses. Sincèrement, cette communauté est exceptionnellement unique, de par son dévouement! =)

Les polynômes de Tchebychev sont une suite de polynômes, telle que le n e polynôme vérifie Tn(cos(t))=cos(nt) pour tout t dans R. On peut montrer très facilement qu'une telle suite de polynômes existe et est unique, que Tn est de degré n et de coefficient dominant 2^n.

C'est vraiment si simple? =3 Elle existe, puisque les Polynômes de Tchebychev sont tels? Son unicité découle directement du fait que la fonction cos (nt) est unique?

Concernant le "monic polynomial", cela dit précisément que si on prend P un polynôme de degré n, qui est unitaire, la plus grande valeur prise par |P| sur [-1,1] est plus grande que 2^-n, et que cette valeur est 2^-n si et seulement si P est plus ou moins Tn/2^n. On divise par 2^n pour obtenir un polynôme unitaire (le coefficient dominant de Tn est 2^n).

Un "monic polynomial" n'est pas un polynôme dont le coefficient directeur est 1? C'est peut être exactement ce que tu dis, mais je suis perdu lorsque tu dis que « la plus grande valeur prise par |P| sur [-1,1] est plus grande que 2^-n ». Est-ce la définition de "monic polynomial"? Ou est-ce un résultat qui découle du fait qu'un "monic polynomial" soit un polynôme dont le coefficient directeur est 1?

Salut,

Si tu cherches des applications de ces polynômes, il y a beaucoup de choses dans le cours de A. Magnus (Ch 2)...

Merci beaucoup! =)

[Le_chat]

C'est vraiment si simple? =3 Elle existe, puisque les Polynômes de Tchebychev sont tels? Son unicité découle directement du fait que la fonction cos (nt) est unique?

Non non, pour démontrer qu'elle existe, il faut dire que comme cos((n+1)t)=2*cos(t)*cos(nt)-cos((n-1)t), si on définit une suite de polynômes par:, et T_1=X, et si n est plus grand que 1, , on a pour tout n Tn(cos(t))=cos(nt) par récurrence, cela montre l'existence de ces polynômes.
Pour l'unicité, si est une suite de polynomes qui vérifie, on a nécessairement , , et si n est plus grand que 1, on en déduit par récurrence que la suite des Qn est la même suite que les Tn , donc que la suite des polynômes Tn est unique.

Un "monic polynomial" n'est pas un polynôme dont le coefficient directeur est 1? C'est peut être exactement ce que tu dis, mais je suis perdu lorsque tu dis que « la plus grande valeur prise par |P| sur [-1,1] est plus grande que 2^-n ». Est-ce la définition de "monic polynomial"? Ou est-ce un résultat qui découle du fait qu'un "monic polynomial" soit un polynôme dont le coefficient directeur est 1?

Je me suis rendu compte que je t'ai dit n'importe quoi plus haut. La traduction de monic polynomial est polynôme unitaire, c'est en effet un polynôme de coefficient dominant égal à 1.
Le problème c'est que les polynomes de tchebychev ne sont pas unitaires, leur coefficient dominant est 2^n. Pour en obtenir un unitaire, il suffit de regarder Tn/2^n, de coefficient dominant 1.

On montre en effet que ce polynôme est le seul (au signe près) polynome de degré n à minimiser la plus grande valeur atteinte par un polynôme sur [-1,1]. Cette valeur vaut en l’occurrence . Une démo se trouve dans le sujet que j'ai linké dans mon premier message.

Cela signifie que si on prend un polynôme unitaire P de degré n, alors on peut trouver un x dans [-1,1] tel que |P(x)| soit supérieur ou égal à 2^-n, et si on ne peut jamais dépasser strictement 2^-n, P est le polynôme Tn/2^n au signe près.

[David R.]

Rebonjour, j'essaie de faire la preuve sur l'unicité, mais je dois, pour cela, montrer que {cos^n(x) | n 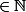} est une famille libre.

En fait, j'ai l'unicité si et seulement si cet énoncé est vrai. Est-ce que je me casse beaucoup trop la tête (car tu semblais dire que l'unicité était facile à montrer) ou, alors, c'est trivial que {cos^n(x) | n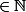 } est une famille libre?

Merci encore,
David

[Doraki]

oui c'est rapide. Suppose que tu as des réels a0 ... an tels que pour tout x, a0 + a1 cos(x) + a2 cos(x)² + ... + an cos(x)^n = 0. Donc tu as un polynôme P à coefficients réels tel que pour tout x, P(cos(x)) = 0.
Donc P(y) = 0 pour tout y dans [-1;1]. Mais le seul polynôme qui a une infinité de racines c'est le polynôme nul, donc P=0 : a0 = a1 = ... = an = 0. Ce qui montre que ta famille est libre.

[David R.]

oui c'est rapide. Suppose que tu as des réels a0 ... an tels que pour tout x, a0 + a1 cos(x) + a2 cos(x)² + ... + an cos(x)^n = 0. Donc tu as un polynôme P à coefficients réels tel que pour tout x, P(cos(x)) = 0.
Donc P(y) = 0 pour tout y dans [-1;1]. Mais le seul polynôme qui a une infinité de racines c'est le polynôme nul, donc P=0 : a0 = a1 = ... = an = 0. Ce qui montre que ta famille est libre.

Merci! =) Par contre, j'ai une question (peut-être métaphysique) qui me frappe. Que vaut ? Je veux dire, ça vaut 1 en général, mais lorsque cos(t)=0 (c'est-à-dire ), la fonction est-elle définie? Est-ce que, par convention, ?

[Le_chat]

La convention pour 0^0 dépend souvent de l'utilisation. Ici, on a envie de dire que cos(t)^0=1 tout le temps, donc la convention 0^0=1.