Question incomprenable (fonction)

par **wYllo30** » 05 Nov 2007, 22:41

[CENTER]Pourai ton m'expliquer la question 4 la deuxieme partie a partir de Soit M et P ...
Je ne comprend pas se que il faud faire.

Merci beaucoup pour m'avancer dans mon probleme[/CENTER]

par **prody-G** » 05 Nov 2007, 22:59

salut tout d'abord,

on te demande la position relative de C et de (D), cad quand C "est au-dessus" de (D) (ie quand f(x)>y) et quand C "est en-dessous" de (D) (ie quand f(x)
M et P sont des points de C et de (D) et ont même abscisse x donc MP représente "l'écart" entre C et (D).
donc MP = |f(x)-y|.

par **wYllo30** » 05 Nov 2007, 23:04

[quote="prody-G"]salut tout d'abord,

on te demande la position relative de C et de (D), cad quand C "est au-dessus" de (D) (ie quand f(x)>y) et quand C "est en-dessous" de (D) (ie quand f(x)10
|x|>100
|x|>1000

que vien faire cela je comprend pas on me demande de calculer l'asymptote ?

par **nuage** » 05 Nov 2007, 23:05

Salut,
comme tu l'a certainement remarqué (D) est asymptote (oblique) à C en +- oo.
La question 4 demande des précisions sur la position de C et (D).
Il est presque évident que si

est positif C est au dessus de (D). Et que (D) est au dessus de C dans le cas contraire.
M et P sont les points dont l'abscisse vérifie

.
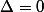
je vois qu'une autre réponse est arrivée.
Fais en ton miel.

par **wYllo30** » 05 Nov 2007, 23:16

nuage a écrit:Salut,
comme tu l'a certainement remarqué (D) est asymptote (oblique) à C en +- oo.
La question 4 demande des précisions sur la position de C et (D).
Il est presque évident que si est positif C est au dessus de (D). Et que (D) est au dessus de C dans le cas contraire.
M et P sont les points dont l'abscisse vérifie .
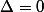
je vois qu'une autre réponse est arrivée.
Fais en ton miel.

mais Pk ca intervien ca sert a koi ca

|x|>10
|x|>100
|x|>1000

par **prody-G** » 05 Nov 2007, 23:23

wYllo30 a écrit:mais POURQUOI ça intervient ça sert à quoi ça ?

|x|>10
|x|>100
|x|>1000

On te demande à partir de quand l'écart entre la courbe et la droite asymptote est inférieur à 1mm soit 0.1, puisqu'il est clair qu'à l'infini l'écart diminue.
Est-ce que pour |x|>10, MP100 ? pour |x|>1000 ?

par **wYllo30** » 05 Nov 2007, 23:33

prody-G a écrit:On te demande à partir de quand l'écart entre la courbe et la droite asymptote est inférieur à 1mm soit 0.1, puisqu'il est clair qu'à l'infini l'écart diminue.
Est-ce que pour |x|>10, MP100 ? pour |x|>1000 ?

Merci ca doit etre sencer ce que tu me dit mais moi je suis a l'ouest bref je pence que une bonne nuit de sommeil pourai eveiller tout cela si tu a une explication plus claire que je peu comprendre re regarde mon probleme la question 4 et essaye de me donner une equation logique je ne comprend pas je me suis embrouiller j'ai rien compri.

Aider moiiiiiiiiiiiiiii

par **nuage** » 05 Nov 2007, 23:36

Salut,

wYllo30 a écrit:mais Pk ca intervien ca sert a koi ca

|x|>10
|x|>100
|x|>1000

Un conseil : si tu lis le français mieux que tu ne l'écris, essaye de lire l'énoncé.
Il s'agit de résoudre :
[TEX]\left|\frac7{x+1}-\frac3{(x+1)^2}\right|10 ?
dès que |x|>100 ?
dès que |x|>1 000?

par **prody-G** » 05 Nov 2007, 23:39

On te demande pas de résoudre une équation, juste de remplacer |x| par 10, par 100 et par 1000 et voir si MP=|f(x)-(x+1)|<0.1.

par **wYllo30** » 05 Nov 2007, 23:48

prody-G a écrit:On te demande pas de résoudre une équation, juste de remplacer |x| par 10, par 100 et par 1000 et voir si MP=|f(x)-(x+1)|<0.1.

Dsl pour mes fautes mais je suis crever j'essaye de resoudre et ca marche po et ca ma souler voila bref je vous remerci bonne soirer je resoudrai demain je remplacerai demain j'ai essaye je trouve des truc bizarre alor je pence aller dormir et on vera demin bn nuit

Question incomprenable (fonction)

question incomprenable (fonction)

Ok mais pourquoi

Ok mais pourquoi

Merci

Merci beaucoup

Qui est en ligne