Bonjour,
J’ai une question un peu bête de compréhension sur les sous groupes (Z/nZ, +).
J’ai vu que les sous groupes de (Z/nZ, +) sont les cla(d) tel que d divise n.
Par exemple, pour (Z/12Z, +), d= 1 2 3 4 6 12.
Mais, dans ce cas, par stabilité, si cla(6) est un sous groupe, en additionnant deux éléments de cla(6), je devrais avoir un élément qui appartient à cla(6). Or, si j’additionne 6+6, on est dans la classe 0.
Voilà pourquoi je ne comprend pas… Avoir une réponse à cette question me permettra d’y voir beaucoup plus clair.
Merci d’avance pour votre aide.
Question de cours sur les sous groupes de (Z/nZ, +)
5 messages
- Page 1 sur 1
Re: Question de cours sur les sous groupes de (Z/nZ, +)
Salut,
Le problème, c'est que visiblement tu as pas bien compris (du tout...) le truc en question.
Pour reprendre les sous groupes de Z/12Z, il y en a effectivement 6 qui sont :
- Le sous groupe engendré par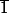 , c'est à dire
, c'est à dire 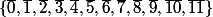 qui a 12 éléments et qui est en fait le groupe tout entier.
qui a 12 éléments et qui est en fait le groupe tout entier.
- Le sous groupe engendré par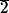 , c'est à dire
, c'est à dire 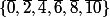 qui a 6 éléments.
qui a 6 éléments.
- Le sous groupe engendré par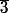 , c'est à dire
, c'est à dire 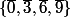 a 4 éléments.
a 4 éléments.
- Le sous groupe engendré par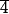 , c'est à dire
, c'est à dire  qui a 3 éléments.
qui a 3 éléments.
- Le sous groupe engendré par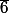 , c'est à dire
, c'est à dire 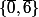 qui a 2 éléments.
qui a 2 éléments.
- Le sous groupe engendré par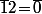 , c'est à dire
, c'est à dire 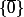 qui a un seul élément.
qui a un seul élément.
Et, évidement, tout les sous groupes contiennent l'élément neutre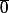 vu que c'est dans la définition même d'un "sous groupe".
vu que c'est dans la définition même d'un "sous groupe".
Le problème, c'est que visiblement tu as pas bien compris (du tout...) le truc en question.
Pour reprendre les sous groupes de Z/12Z, il y en a effectivement 6 qui sont :
- Le sous groupe engendré par
- Le sous groupe engendré par
- Le sous groupe engendré par
- Le sous groupe engendré par
- Le sous groupe engendré par
- Le sous groupe engendré par
Et, évidement, tout les sous groupes contiennent l'élément neutre
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Question de cours sur les sous groupes de (Z/nZ, +)
Ok merci beaucoup.
Donc, pour le cas générale, puisque selon le théorème de Lagrange, le cardinal d'un sous groupe divise le cardinal du groupe, une condition éliminatoire est que le sous groupe soit engendré par un élément qui divise n?
Mais ça ne suffit pas à démontrer que les sous groupes de (Z/nZ, +) sont les Z/dZ j'imagine...
Donc, pour le cas générale, puisque selon le théorème de Lagrange, le cardinal d'un sous groupe divise le cardinal du groupe, une condition éliminatoire est que le sous groupe soit engendré par un élément qui divise n?
Mais ça ne suffit pas à démontrer que les sous groupes de (Z/nZ, +) sont les Z/dZ j'imagine...
Re: Question de cours sur les sous groupes de (Z/nZ, +)
Je comprend pas trop ce que tu veut dire avec tes "condition éliminatoire"...
Sinon, il faut bien comprendre que si tu prend un entier qui ne divise pas
qui ne divise pas  tu as parfaitement le droit de considérer le sous groupe de Z/nZ engendré par
tu as parfaitement le droit de considérer le sous groupe de Z/nZ engendré par 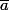 et que ça sera évidement... un sous groupe. Par contre, ce que te dit le théorème, c'est que ce sous groupe engendré par
et que ça sera évidement... un sous groupe. Par contre, ce que te dit le théorème, c'est que ce sous groupe engendré par 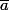 , il sera aussi engendré par un (unique)
, il sera aussi engendré par un (unique) 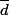 tel que
tel que  soit un diviseur positif de
soit un diviseur positif de  .
.
Par exemple, avec Z/12, tu peut évidement considérer le sous groupe engendré par exemple par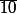 , mais c'est le même que celui engendré par
, mais c'est le même que celui engendré par 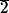 .
.
De même, celui engendré par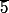 , c'est le même que celui engendré par
, c'est le même que celui engendré par 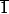 (c'est à dire Z/12Z tout entier)
(c'est à dire Z/12Z tout entier)
Sinon, concernant la preuve, on peut le faire "plus ou moins à la main", mais avec un tout petit peu de théorie, c'est immédiat :
Si est un sous groupe de Z/nZ, on considère la surjection canonique
est un sous groupe de Z/nZ, on considère la surjection canonique 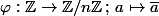 qui est évidement un morphisme de groupe.
qui est évidement un morphisme de groupe.
L'ensemble) est donc un sous groupe de
est donc un sous groupe de 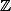 ce qui signifie qu'il existe
ce qui signifie qu'il existe 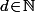 tel que
tel que \!=\!d{\mathbb Z}) .
.
De plus, comme\!=\!\overline n\!=\!\overline 0\!\in\!H) (car
(car  est un sous groupe), on a
est un sous groupe), on a \!=\!d{\mathbb Z}) ce qui signifie que
ce qui signifie que  divise
divise  .
.
Enfin, comme est surjective, on a
est surjective, on a 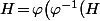\big)\!=\!\varphi\big(d{\mathbb Z}\big)\!=\!\{k\overline{d}:k\!\in\!{\mathbb Z}\}) ce qui signifie que
ce qui signifie que  est le sous groupe engendré par
est le sous groupe engendré par 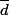 , et que
, et que 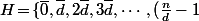\overline {d}}\}) (qui a n/d éléments}
(qui a n/d éléments}
De plus, si et
et  sont deux diviseurs positifs distincts de n, les sous groupes de Z/nZ engendré par
sont deux diviseurs positifs distincts de n, les sous groupes de Z/nZ engendré par 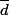 et
et 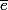 seront distinct (car le premier a n/d éléments et le deuxième en a n/e) et cela signifie qu'il y a une bijection entre les sous groupes de Z/nZ et les diviseurs (positifs) de n.
seront distinct (car le premier a n/d éléments et le deuxième en a n/e) et cela signifie qu'il y a une bijection entre les sous groupes de Z/nZ et les diviseurs (positifs) de n.
Sinon, il faut bien comprendre que si tu prend un entier
Par exemple, avec Z/12, tu peut évidement considérer le sous groupe engendré par exemple par
De même, celui engendré par
Sinon, concernant la preuve, on peut le faire "plus ou moins à la main", mais avec un tout petit peu de théorie, c'est immédiat :
Si
L'ensemble
De plus, comme
Enfin, comme
De plus, si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Question de cours sur les sous groupes de (Z/nZ, +)
Ok merci pour ces infos. Je vais essayer de retrouver la démonstration avant de lire la tienne.
Merci
Merci
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
