Question con (sic)

[Sourire_banane]

Salut,

Comment justifier qu'une matrice de taille 2*2 ait forcément un indice de nilpotence de 2 si elle est nilpotente ?
Merci

[Doraki]

Ben non, la matrice nulle est nilpotente d'indice 1.

Si A est nilpotente d'indice m alors X^m est le polynome minimal de A. Maintenant comme le polynôme caractéristique de A (qui est de degré n) annule aussi A, on a donc n >= m.

[Monsieur23]

Aloha,

On va rajouter "non nulle".

Ensuite, tu sais que si une matrice est nilpotente, alors son indice de nilpotence est majoré par la dimension de l'espace. Donc, ici, 2.

[Sourire_banane]

Aloha,

On va rajouter "non nulle".

Ensuite, tu sais que si une matrice est nilpotente, alors son indice de nilpotence est majoré par la dimension de l'espace. Donc, ici, 2.

La dimension de M2(R) c'est pas 4 ?

Et Doraki, j'ai pas la notion de polynôme minimal dans mon cours.

Pour vous expliquer un peu le contexte, je dois montrer que si une matrice de M2(R) est nilpotente, alors on a phi(A)=0 (avec pour tous (A,B) dans M2(R)², phi(AB)=phi(A)phi(B) et phi non constante).
Dans la correction, ya marqué que si A est nilpotente, alors A²=0 car A est de taille 2.

[Ben314]

Salut,
Pour montrer "à la main" ce que dit Doraki, à savoir que, si une matrice de est nilpotente d'ordre alors on peut procéder de cette façon :
Comme est la plus petite puissance telle que , c'est que est non nulle donc on peut trouver un vecteur colonne tel que . Par contre, évidement, vu que .
Il est alors facile de voir que la famille est libre :
Si alors, en composant (à gauche) par , on obtient vu que pour tout et, comme , cela montre que .
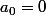En composant (à gauche) par , on obtient vu que 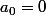et que pour tout donc .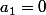
etc...
Et on conclue en disant que, vu qu'on est dans un espace de dimension , une famille libre a au plus éléments donc .

[Sourire_banane]

Merci pour ta réponse Ben314 !