Question chaude

par **Anonyme** » 21 Fév 2006, 14:33

hello...c est un resultat qu un pote m a cité,mais qui ne semble pas evident..voila:soit f de R dans R.montrer que si f^2 et f^3 sont infiniment derivable,alors f l'est ossi...qqun a une idee?

par **hild** » 21 Fév 2006, 14:55

Tu as f^2 dérivable, f^3 dérivable. Cela implique, sur tout intervalle sur lequel f ne s'annule pas, 1/f^2 est infiniment dérivable, et par suite, f^3/f^2=f aussi...

En effet, si f et g dérivables, leur produit aussi...

par **yos** » 21 Fév 2006, 15:43

Et si f s'annule?

par **El_Gato** » 21 Fév 2006, 15:46

yos a écrit:Et si f s'annule?

C'est bien là qu'est le pb, si l'énoncé est correct et si ce n'est pas un hoax.

par **yos** » 21 Fév 2006, 17:52

Je pense que l'énoncé est correct et son seul intérêt réside dans le cas où f s'annule.

par **redwolf** » 21 Fév 2006, 18:42

Bonjour.

Je crois que ce n'est pas un hoax. On pourrait commencer par prouver que f est dérivable. Même ça ce n'est pas évident...

par **nuage** » 21 Fév 2006, 19:11

Salut,
On peut considérer le contre-exemple f(x)=|x|

par **yos** » 21 Fév 2006, 21:32

nuage a écrit:Salut,
On peut considérer le contre-exemple f(x)=|x|

|x|^3 est pas 3 fois dérivable en 0

par **nuage** » 21 Fév 2006, 22:37

Salut,

yos a écrit:|x|^3 est pas 3 fois dérivable en 0

j'avais mal lu la question :briques:

par **cesar** » 22 Fév 2006, 13:00

yos a écrit:Je pense que l'énoncé est correct et son seul intérêt réside dans le cas où f s'annule.

il faut prolonger par continuité : à gauche et à droite de 0, elle est derivable ...

par **El_Gato** » 22 Fév 2006, 13:13

cesar a écrit:il faut prolonger par continuité : à gauche et à droite de 0, elle est derivable ...

Il n'y a rien à prolonger: sur

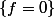
les valeurs de f sont imposées et valent... 0.

Tout le problème est de montrer que les conditions sur

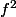
et

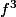
impliquent un bon comportement sur la frontière du fermé

.

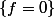
Cet exercice m'intrigue: je n'ai pas encore la preuve, mais je ne trouve pas de contre-exemple non plus.

par **chulzi** » 22 Fév 2006, 19:16

je vois que je nage dans la cour des grands !!!!!

bon si on pose g(x) = (f(x))² on a alors g'(x) = 2f(x) f'(x) comme g est n fois dérivable, alors g'(x) est au minimum (n-1) dérivable est on aura à la fin la dérivé nième de f(x), peut être que c'est juste sa.

par **El_Gato** » 22 Fév 2006, 19:20

chulzi a écrit: si on pose g(x) = (f(x))² on a alors g'(x) = 2f(x) f'(x) comme g est n fois dérivable, alors g'(x) est au minimum (n-1) dérivable est on aura à la fin la dérivé nième de f(x), peut être que c'est juste sa.

Non, tu ne peux écrire

que si u et v sont toutes deux dérivables. Un produit peut être dérivable sans que les termes du produit le soient:

.

par **chulzi** » 22 Fév 2006, 19:44

El_Gato a écrit:Non, tu ne peux écrire que si u et v sont toutes deux dérivables. Un produit peut être dérivable sans que les termes du produit le soient: .

comme f² est dérivable est f^3 dérivable et f^3= f²*f alors si f n'est pas dérivable donc f^3 n'est pas dérivable. c juste sa???????????!!!!!!!!

par **nuage** » 22 Fév 2006, 19:50

Salut,

chulzi a écrit:comme f² est dérivable est f^3 dérivable et f^3= f²*f alors si f n'est pas dérivable donc f^3 n'est pas dérivable. c juste sa???????????!!!!!!!!

Voir le contre-exemple f(x)=|x| (faux, mais il est effectif dans ce que tu proposes) que j'ai posté un peu plus haut.
A+

par **chulzi** » 22 Fév 2006, 19:57

je ne te comprend pas, moi je voulais faire une preuve par l'absurde c'est tout. si tu pouvais m'expliqué ce serait chic de ta part.

par **nuage** » 22 Fév 2006, 20:04

Salut,

est dérivable en zéro.

n'est pas dérivable en zéro.

On a besoin de f^3 infiniment (ou au moins 3 fois) dérivable.

par **Yipee** » 23 Fév 2006, 00:39

C'est un exercice connu (mais je ne m'en souviens plus) et (très) difficile. Je me souviens qu'il y avait une démo de 2 ou 3 pages dans un RMS.

par **Anonyme** » 01 Mar 2006, 15:30

yipee,est ce que tu sais dan quel rms on peut trouver ca?..

par **Yipee** » 03 Mar 2006, 08:37

En fait j'ai l'article en pdf je peux donc le mettre quelque part ou je peux essayer de donner des explications mais c'est assez long.

Question chaude

question chaude

Qui est en ligne