au départ, il y a la distributivité simple de la multiplication sur l'addition:
 = 3 \times 5 + 3 \times 2)
ce que l'on écrit avec des littéraux
=ka+kb)
(le signe de multiplication ne s"écrit pas)
avec 4 littéraux a,b,c,d
pour calculer (a+b)(c+d) (produit de deux sommes)
on pose k=a+b
(a+b)(c+d)=k(c+d)=kc+kd
(a+b)(c+d)=(a+b)c+(a+b)d=ac+bc+ad+bd
(a+b)(c+d)=ac+bc+ad+bdcette dernière formule doit ête connue par coeur...
exemple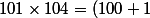(100+4)=10 000 +100+400+4=10 504)
notation d'un carré
on note
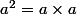
cas particulier(a+b)(c+d)=ac+bc+ad+bd
quand c=a et d=b , à gauche du signe égal, on obtient
^2)
à droite
d'où la 1ère identité remarquable
^2=a^2+2ab+b^2)
il y en a deux autres qui se démontrent aussi en utilisant la double distributivité:
^2=a^2-2ab+b^2)
et enfin
(a+b)=a^2-b^2)
l'égalité étant symétrique, cette dernière identité s'écritt aussi
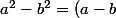(a+b))
on dit que l'on sait factoriser la différence de deux carrésexemple:
1er produit de la question 2(- \frac{1}{3} a + \frac{1}{2}b))
on effectue mentalement un changement de variable,ie, un changement de notation, pour voir la structure
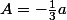
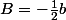
le produit:
a la structure
(A+B)(A-B)
que l'on développe en
(A-B)=A^2-B^2)
d'où
(- \frac{1}{3} a + \frac{1}{2}b)= \left( - \frac{1}{3} a \right)^2 - \left( - \frac{1}{2} b \right)^2= \frac{1}{9} a^2 - \frac{1}{4}b^2)
