Quelques petites questions

[Aziliz]

[FONT=Arial]Bonjour je vous soumets un début d’exercice sur lequel je bûche mais j’ai de gros problèmes qui se posent à moi. Je demande pas qu’on le fasse à ma place mes des indices me seraient utiles ![/FONT]

[FONT=Palatino Linotype]On désigne par n un entier naturel non nul et a un réel strictement positif
On se propose d’étudier les racines de l’équation :
(En) : (1/x)+(1/x+1)+(1/x+2)+…+(1/x+2n)=a

A cet effet on introduit la fonction fn, de la variable x définie par :

fn(x)= (1/x)+(1/x+1)+(1/x+2)+…+(1/x+2n)-a

I -1 Dresser le tableau de variations de fn
2 Justifier l’existence de racines de l’équation (En) et en déterminer le nombre

II-On note xn la plus grande des racines de (En)
1-Justifier que xn>0
2- Démontrer que pour tout réel x>1
1/x < ln(x/(x-1)) < 1/(x-1)

En déduire que pour tout réel x strictement positif

fn (x) – (1/x) +a < ln(1+(2n/x)) < fn(x)-( 1/(x+2n))+a[/FONT]

[FONT=Arial]Voilà alors mon dilemme se trouve dans le fait que d’après moi la dérivée de f serait négative en tant que somme de nombres négatifs mais cela est impossible car alors la fonction serait décroissante or ses limites en + et –oo sont égales toutes les 2 à (–a) donc la fonction ne peut être strictement décroissante mais je ne vois pas mon erreur dans le calcul de dérivée.
Ensuite j’aimerais une piste pour la justification du fait que xn est strictement positive car je ne vois pas du tout pourtant ça ne doit pas être très difficile j’ai essayé de me servir du fait que a est positif mais ça ne m’aide pas pour l’instant.
Enfin je crois que pour la première inégalité avec le logarithme népérien il faut utiliser les inégalités des accroissements finis or je ne vois pas comment m’y prendre.
Voilà si vous pouviez me donner quelques pistes ce serait gentil car je bute vraiment et à force de réfléchir je n’ai aucun recul et je n’avance pas or l’exercice continue et j ‘aimerais en venir à bout !
Je vous remercie par avance.[/FONT]

[Sdec25]

Salut
Il n'y a pas d'erreur dans le calcul de la dérivée, la fonction est décroissante et tend vers -a

Pour montrer qu'il y a au moins une racine positive, calcule la limite en 0+ et la limite en , sachant que la fonction est continue tu peux déduire qu'il y a au moins une racine positive.

Pour les ln utilise le théorème des accroissements finis entre a et b avec a=x-1 et b=x
Entre x-1 et x il existe une dérivée égale à
Calcule la dérivée de ln(x), et encadre la par rapport à la dérivée en a et en b (sachant que a<x<b) et tu devrais trouver ton encadrement.

[Aziliz]

Merci beaucoup pour ton aide j'ai réussi à trouver mon encadrement!c'est très gentil!
Mais juste un truc si la fonction est décroissante strictement sa limite en -oo n 'est pas -a comme je le croyais mais alors quelle est -elle? +a peut-être?je m'embrouille un peu je crois. De plus si elle est décroissante il n'y a alors qu'une seule racine non?c'est possible mais comme l'énoncé parle de plusieurs racines j'avais cru qu'il y en aurait plusieurs...mais bon ça ça ne veut rien dire l'énoncé n'allait pas me donner la réponse!
En tout cas merci beaucoup pour les pistes cela m'a beaucoup éclairé et si quelqu'un pouvait me montrer pourquoi je m'égare encore ainsi avec les limites et les racines ce serait très gentil!

[Sdec25]

De rien :zen:
En fait la fonction est décroissante si x est positif et croissante si x est négatif (au voisinage de l'infini), mais pas croissante sur car elle n'est pas définie sur cet intervalle, et il peut y avoir plusieurs racines.

De plus la limite est la même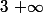 en et en .

edit : rectification, elle est toujours décroissante (sur les intervalles où elle est définie), et elle est continue sur

[Chimomo]

Il faut faire attention au domaine de définition de f, elle est définie sur une réunion d'intervalles ouverts puisqu'ellen'est définie pour aucun entier entre 0 et -2n .

[Aziliz]

Oui merci à tous les deux! je viens de m'apercevoir qu'il y avait plus de valeurs interdites que je ne le croyais... c'est tellement évident que je n'ai rien vu du tout!!J'ai honte!!
Du coup je comprend mieux pourquoi il y a plusieurs racines...j'avoue ne pas être bien sûr du nombre encore, je croyais 2n+1 mais je ne suis pas très sûre...
En plus là je bûche pour transformer l'encadrement que j'ai trouvé grâce à l'aide judicieuse de Sdec25 je crois voir une solution à chaque fois mais la transformation du ln me bloque tout...
En tout cas merci beaucoup de votre aide j'y vois bien plus clair à présent sur cette fonction qui bien que pas si difficile m'a longtemps perturbée!!C'est très gentil à vous!

[Sdec25]

De rien ;)
Où est-ce que tu bloques précisément ?

[Aziliz]

c'est fou ce que cet exercice aura demandé comme questions je suis désolée!!
j'ai encore une petite question de vocabulaire on me dit de déterminer le nombre de racines...je dois faire une belle démonstration à votre avis?je n'espère pas car je n'ai jamais prouvé ce genre de choses...

Ensuite ma dernière question(et après je laisse tout le monde tranquille)
j'ai trouvé l'encadrement donc avec les inégalités des accroissements finis(merci^^)et ensuite on me demande de trouver l'autre expression.

[FONT=Palatino Linotype]1/x (1/x+1)+...+(1/(x+2n)) et pareil avec le membre de droite mais en fait le ln change aussi donc ça ne marche pas...il doit juste y avoir une petite astuce puisqu'il y a écrit que je dois juste déduire l'encadrement du précédent pourtant je ne vois pas, il faut peut-être appliquer la fonction quelque part...je ne sais pas s'il faut ajouter de part et d'autre f(n) puis (+a) jusqu'a trouver la nouvelle expression ou alors il faut se servir de l'expression que j'ai trouvé en effectuant f(n)-(1/x)+a...je n'arrive pas du tout à voir clair dans cet exercice pourtant il est censé juste me faire réviser...humhum
en tout cas désolée de poser autant de questions mais j'ai vraiment envie de comprendre!merci de votre patience :happy2:

[Sdec25]

pas de problème :happy3:
On a ce qui équivaut à

Essaie de faire la somme de ces expressions pour k allant de x+1 à x+2n
"ln k - ln(k-1)" est une suite télescopique, il ne reste que le premier et le dernier terme si tu fais la somme.

Pour trouver le nombre de racines il y a sûrement une question qui peut t'aider. Je n'ai pas l'énoncé en tête mais on peut étudier les variation de la fonction : la fonction est définie sur les intervalles ]n, n+1[ (n entier), et si la fonction est strictement croissante ou décroissante sur cet intervalle, et coupe l'axe des abscisses (par exemple si les valeurs vont de à ) alors il y a 1 solution par intervalle de ce type.

Si tu as d'autres questions n'hésite pas :happy2:

[Aziliz]

[FONT=Georgia]Désolée mais j'ai bien une question encore...

Je dois montrer que xn > (2n/(exp a –1))
Je précise que le n de xn est un indice alors que le n de 2n est une multiplication

J’ai trouver grâce à une question de l’exo que

a – (1/xn) (2n/ (exp(a)-1)
xn * (exp(a) –1) > 2n (je ne sais pas si l’on doit inverser le sens de l’inégalité il faudrait en savoir plus sur exp(xn))
xn * exp(a) - xn > 2n
xn * exp(a) > 2n + xn

les deux expressions que j’ai trouvé sont très proches et pourtant je n’arrive pas à les rejoindre il faudrait que exp(xn) soit égale à 1 ou (–1) mais je ne vois pas comment on sait cela…
Ou peut-être que je fais simplement fausse route…quelqu’un voit-il l’astuce ??
Merci d’avance et désolée de tant de questions d’un coup !![/FONT]

[nox]

exp (a) * exp (- (1/xn))< exp (ln (1+(2n/xn))
exp (a) * exp(xn) < 1+ (2n/xn)

comment fais tu ce passage? exp(-1/xn) n'est pas égal à exp(xn)

quelles sont les conditions sur xn?(dans quel ensemble est-il choisi etc...)

je ne vois pas apparaître de "xn" dans les questions précédentes...d'où sortent ils?

[Aziliz]

alors xn c'est la plus grande racine de l'expression (En)
(En): (1/x)+ (1/(x+1))+...+(1/(x+2*n))=a
on sait juste que xn est strictement supérieur à zéro

je ne sais plus comment j'ai fait le passage je suis partie de exp(-a)=1/exp(a)
donc exp(- 1/xn)=1/exp(1/xn)...et oui je ne sais pas comment je suis arrivée là c'est faux tu as raison!merci!

donc on a les deux expressions

xn*exp(a)*(1/(exp(1/xn)))
et xn*exp(a)>2*n + xn...je ne sais pas si j'ai utilisé la bonne méthode mais ça me semblait se rapprocher de la solution!

[Aziliz]

Bon apparemment ça n'inspire personne!lol!
Pensez-vous au moins que je sois partie dans la bonne direction?le vrai problème c'est que l'on sait peu de choses sur xn!!
En tous les cas si quelqu'un pense qu'il y a une autre voie pour démontrer que xn> (2n/(exp(a)-1)) n'hésitez pas!!!
Merci d'avance!