Quelle fonction pour ce graphe Courbes de BEZIER

par **ckoi** » 07 Déc 2007, 09:41

Bonjour,

Je cherche la fonction f(x) qui permettrait de tracer ce graphe.
Cliquez ici pour afficher le graphe
Les 4 points P0, P1, P2, P3 sont variables
Ca doit être assez simple avec des courbes de BEZIER mais je cale

Avez vous une piste ?

Merci

par **abcd22** » 07 Déc 2007, 10:01

Bonjour,
Le lien ne fonctionne pas chez moi (réponse HTTP incorrecte).

par **xyz1975** » 07 Déc 2007, 12:06

Bonjour,
Est ce que vous avez des propriètés de f ou alors n'importe quel renseignements?

par **ckoi** » 07 Déc 2007, 15:22

xyz1975 a écrit:Bonjour,
Est ce que vous avez des propriètés de f ou alors n'importe quel renseignements?

F doit passer par les points remarquables indiqués dans le graphe

par **ckoi** » 07 Déc 2007, 20:29

Quelqu'un aurait-il une idée ?
C'est vraisemblablement dans les courbes de BEZIER que ce trouve la solution mais je n'y arrive pas

par **nuage** » 08 Déc 2007, 07:55

Salut,
il y a une fonction polynôme de degré 3 qui passe par les 4 points.
On peut l'écrire assez facilement avec les polynômes de Lagrange.

Avec

coordonnées de

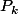
Mais il n'est pas certain que ça convienne bien : il n'y a pas de contrôle sur l'aspect de la courbe.

par **ckoi** » 08 Déc 2007, 09:06

Nuage,

Merci pour votre réponse.
Il y a vraisemblablement plusieures solutions
Diffrentes pistes sont possibles.
Je pensai également à un équivalent "cycloïde"

par **ckoi** » 08 Déc 2007, 09:09

Nuage,

Comment faites vous pour ecrire les formules avec une excellente présentation ?

par **ckoi** » 08 Déc 2007, 14:11

Est-ce un pb insoluble ?

par **nuage** » 09 Déc 2007, 09:51

ckoi a écrit:Nuage,

Comment faites vous pour ecrire les formules avec une excellente présentation ?

Vous pouvez me tutoyer.
Pour les formules j'utilise TEX
Il y a un lien utile dans ma signature.

Quelle fonction pour ce graphe Courbes de BEZIER

Quelle fonction pour ce graphe Courbes de BEZIER

Qui est en ligne