Quaternion ==> Rotation axes angles

[Anto75000]

Bonjour à tous,

Après m'être plusieurs fois reporté sur internet, je n'ai pas encore trouvé réponse à ma question:

comment passer d'un quaternion rotation q= [a b c d]

à un ensemble d'axe x,y,z + 3 valeurs de rotation.

??


Merci d'avance pour vos réponses bienvenues !

[Ben314]

Salut,
Je ne comprend pas trop la question....
L'ensemble de quaternions c'est le corps gauche formé muni de l'addition "terme à terme" et du produit défini par .
On peut "couper" les quaternions en une partie "réelle"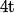 et une partie "vectorielle" et on voit qu'alors le produit s'exprime sous la forme où désigne le produit scalaire et le produit vectoriel.
Ensuite, dans l'espace vectoriel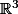 , la rotation (vectorielle) d'axe (unitaire) et d'angle 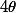, c'est l'application et, en terme de quaternions, ça correspond à la conjugaison par le quaternion (unitaire) , c'est à dire à l'application où
Regarde sur wiki si tu veut plus de détails.

[sylvainc2]

Je pense que tu veux convertir une rotation 3D de la forme quaternion à la forme angles d'Euler, c'est çà?

La première étape est de convertir à la forme matrice de rotation 3D comme indiqué ici:
https://fr.wikipedia.org/wiki/Quaternions_et_rotation_dans_l%27espace#D.27un_quaternion_en_matrice_orthogonale

Ensuite on extrait les angle d'Euler de cette matrice dans l'ordre voulu (il y a plusieurs possibilités) comme indiqué dans ce pdf:
http://www.geometrictools.com/Documentation/EulerAngles.pdf

Je pense que l'ordre x,y,z est le chapitre 2.6 car si tu utilises des vecteurs colonnes (donc multiplication par la droite) alors il faut multiplier les matrices individuelles dans l'ordre Rz*Ry*Rx