Quantificateur, implication

[nico2b]

Voici l'énoncé :

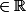
Soient a,b . Si >0, |a-b| , alors a = b.

JE ne vois pas trop comment m'en sortir pour prouver cette affirmation...

Comme |a-b| , on a que - mais je ne sait pas aller plus loin...

Merci d'avance pour l'aide

[fahr451]

il y a deux façons de démontrer

1) prendre une suite d 'epsilon qui tend vers 0 epsilon = 1/n
pour tout n >0 l a-bl =<1/n on passe à la limite et on a l a -b l =<0 donc a = b

2) par l absurde
on suppose a différent de b donc l a-b l >0

on pose epsilon = l a-bl /2 pour cet epsilon là on n ' a pas
l a-bl= < epsilon absurde.

[nico2b]

Ok j'ai compri merci à vous

[mathelot]

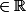
Soient a,b . Si >0, |a-b| , alors a = b.

ou alors tu prends ça comme la définition de l'égalité de deux réels puisque
l'ensemble des réels n'est autre que l'ensemble des suites de cauchy de rationnels quotienté par l'idéal des suites de rationnels tendant vers zéro.