Re bonjour
Avec la méthode de gauss
Par exemple
q(x,y,z)= xz + 2yy² + 2z² + 2xy - 4xz - 6yz
je trouve comme décomposition
(x+y-2z)² + (y-z)² - 3(z²)
donc ma nouvelle base c'est X,Y,Z
avec X= x+y+2z
Y = y-z
Z= z
mais c'est pas une base ortogonale ça ?
Quadrique
11 messages
- Page 1 sur 1
par XENSECP » 11 Jan 2009, 15:36
Pour avoir une base il faudrait des vecteurs :) Là tu as juste réduis la quadrique :)
par sOft007 » 11 Jan 2009, 15:37
mais mais comment je la trouve ma base alors ????
:cry: :cry: :cry:
je désespère...
:cry: :cry: :cry:
je désespère...
par sOft007 » 11 Jan 2009, 15:40
si je fait x= xe1 + ye2 + ze3 = Xa1 + Ya2+Za3
= a1(x+y-2z) + a2( y-z) + a3 (z)
= x (a1) + y(a1 + a2) + z (-2a1 -a2 +a3)
je dis alors que
e1 = a1
e2= a1+a2
e3 = -2a1 -a2 +a3
donc a1 = e1
a2 = e2-a1
a3=...
a1 a2 a3 ma nouvelle base ??
= a1(x+y-2z) + a2( y-z) + a3 (z)
= x (a1) + y(a1 + a2) + z (-2a1 -a2 +a3)
je dis alors que
e1 = a1
e2= a1+a2
e3 = -2a1 -a2 +a3
donc a1 = e1
a2 = e2-a1
a3=...
a1 a2 a3 ma nouvelle base ??
par Antho07 » 11 Jan 2009, 20:51
Ok tu as effectué la méthode de Gauss et tu aboutis (je vérifie pas les calculs) à
=(x+y-2z)^{2}+(y-z)^{2}-3z^{2})
Notons au passage que la signature est (2,1)
Maintenant il faut trouver la base:
Pour l'instant on a l'expression de 3 formes linéaires:
&=&x&+&y&-&2z \\<br /> L_{2}(x,y,z)&=&&&y&-&z \\<br /> L_{3}(x,y,z)&=&&&&&z <br />\end{array})
Il faut chercher la base antédual de
.
Pour ce faire, on remarque que si (e1,e2,e3) désigne la base canonique de E
alors
on a
On veut donc trouver l'antéduale de (L1,L2,L3)
Pour l'instant on le shema suivant:
& \stackrel{Q}{\rightarrow}& ( \ldots,\ldots,\ldots)\\ (e_{1}^{\ast},e_{2}^{\ast},e_{3}^{\ast})&\stackrel{P}{\rightarrow}&(L_{1},L_{2},L_{3}) \end{array})
ou Q et P désigne la matrice de passage.
Ce que l'on cherche c'est Q en faite.
Si on a Q , on aura la base antéduale de (L1,L2,L3) exprimé dans la base canonique.
Or un théorème ou propriété je sais plus dit que
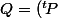^{-1})
Donc pour trouver la base antéduale , on inverse le systeme et on prend la transposé.
Dans ton exemple:
Et maintenant on tanspose donc on obtient comme antédual finalement (je note les vecteurs en ligne)
)
(1L1 premiere ligne, 0 deuxieme , 0 troisieme)
)
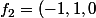(-1L2 premiere ligne, 1 L2 deuxieme, 0 troisieme)
)
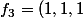La base recherché est la base)
(on vérifie qu'elle marche bien)
En espérant avoir été clair
Notons au passage que la signature est (2,1)
Maintenant il faut trouver la base:
Pour l'instant on a l'expression de 3 formes linéaires:
Il faut chercher la base antédual de
Pour ce faire, on remarque que si (e1,e2,e3) désigne la base canonique de E
alors
on a
On veut donc trouver l'antéduale de (L1,L2,L3)
Pour l'instant on le shema suivant:
ou Q et P désigne la matrice de passage.
Ce que l'on cherche c'est Q en faite.
Si on a Q , on aura la base antéduale de (L1,L2,L3) exprimé dans la base canonique.
Or un théorème ou propriété je sais plus dit que
Donc pour trouver la base antéduale , on inverse le systeme et on prend la transposé.
Dans ton exemple:
Et maintenant on tanspose donc on obtient comme antédual finalement (je note les vecteurs en ligne)
La base recherché est la base
(on vérifie qu'elle marche bien)
En espérant avoir été clair
par Clembou » 11 Jan 2009, 22:33
sOft007 a écrit:la base f1 f2 f3 n'est pas ORTHOGONALE !
Tu connais le procédé de Gram-Schmidt pour orthonormalisé une base ? Tu utilises ce procédé pour orthonormalsé la base
par Antho07 » 11 Jan 2009, 23:11
Ha mais d'accord tu cherches une base orthogonal pour q et orthormal pour le produit scalaire.......c'etait ambigu désolé....
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :