Puissances de nombres premiers

[Craw]

Un autre exemple intéressant :

alors
Ici mais F(n) n'est pas premier donc on calcule Ici p=47 et k=6

[Craw]

Salut,
A mon avis, vu que je ne pense pas qu'il y ait le moindre lien entre les propriétés (de congruence) d'un nombre premier et son numéro , pour qu'une telle conjecture ait (un peu) du sens, il faut commencer par remplacer le par un premier quelconque.
Par contre, le , vu sa nature particulière (au niveau divisibilité) il ne faut pas le remplacer par un entier tout à fait quelconque.

Et sinon, je ne vois pas trop à quoi ça pourrait bien mener d'intéressant une telle conjecture, même si elle était vraie : quelle lien a-t-elle avec les problème intéressantes de l'arithmétique ?

Salut,

Quand j'avais testé avec un programme, quand je remplaçais par ça ne marchait plus, également avec d'autres n. Apparemment la conjecture est vérifiée uniquement avec .

Concernant le caractère intéressant ou pas de la formule ça reste une petite conjecture que j'ai trouvée, bien entendu que ça ne révolutionnera pas les maths.

[stfj]

Tu peux poser le problème sur Les-mathématiques.net ou, si l'anglais ne t'arrête pas, sur math stack exchange. Nul doute que ce problème en intéressera plus d'un. Je peux le faire à ta place si tu veux.

[Craw]

Tu peux poser le problème sur Les-mathématiques.net ou, si l'anglais ne t'arrête pas, sur math stack exchange. Nul doute que ce problème en intéressera plus d'un. Je peux le faire à ta place si tu veux.

Je l'avais déjà posé sur math stack exchange à l'époque, j'ai reçu 12 like mais ça dépassait tout le monde, aucune démo n'avait été faite.

[stfj]

Tu m'étonnes pour les 12 like ! C'est cool comme conjecture. Et sur les mathématiques.net ?

[stfj]

Quel est le titre sur MSE que je retrouve le msg ?

[Craw]

Voici le lien mathoverflow (et j'avais 10 like pas 12) : https://mathoverflow.net/questions/4618 ... -of-primes

Ne tiens pas compte de car cette partie est fausse. Il faut tenir compte de .

[stfj]

@Ben314 : bonjour, je vois au moins un intérêt à cette conjecture. Si on en fait un exercice, cela oblige les étudiants à tester pour différentes petites valeurs de et à se familiariser ainsi avec la fonction caractéristique d'Euler, son calcul, celui du calcul de la somme des diviseurs de , une petite congruence sympathique modulo 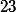, une utilisation éventuelle du théorème de la progression arithmétique de Dirichlet pour prendre conscience du fait qu'il y a une infinité de nombres premiers dans la classe , l'observation éventuelle de ... Bref un exercice répétitif de calcul où on se familiarise avec tout cela. Cordialement, Stéphane

[stfj]

Tu peux faire confiance à Gerry Myerson et Peter sur Math stack Exchange. Ta conjecture est toujours d'actualité. Et s'ils ne sont pas parvenus à la prouver, je laisse tomber.

[stfj]

Et Bill Dubuque a forcément jeté un coup d'oeil aussi. Et là, on change de sphères. Si tu t'acharnes dessus, tu risques de t'y casser les dents.

[Craw]

J'ai envoyé ma conjecture à mon ancien prof de maths de terminale S (ça remonte à 2008 maintenant). Il m'a redirigé vers un maitre de conférence mais celui-ci est très occupé. Donc parfois je le relance mais il est occupé.

C'est pour ça qu'on ne pourrait même pas en faire un exercice car pour démontrer cette conjecture il faut y aller.

[stfj]

Maintenant tu es à 11 sur mathoverflow

[Craw]

Maintenant tu es à 11 sur mathoverflow

Merci si ça vient de toi.

[stfj]

Non tu n'as pas compris le sens de ma remarque à Ben314. Ta conjecture, personne n'est parvenue à la démontrer(même pas Bill Dubuque). Donc aucun espoir de la démontrer par des moyens élémentaires probablement. Si tant est qu'elle soit vraie ! Par contre, tant que n'existe pas de contre-exemple, on peut la présenter comme une conjecture valide et proposer de la tester sur n'importe quel entier. Ces tests constitueraient l'exercice dont je parle, un exercice très répétitif permettant de se familiariser avec les objets mathématiques qu'elle utilise. Ou encore pour un professeur d'informatique, l'occasion de créer un exercice pour ses élèves pour vérifier la conjecture pour des entiers.

Le plus raisonnable selon moi, est d'abandonner tout espoir de la démontrer (si tant est qu'elle est vraie). Et de la laisser à beaucoup plus costaud sur mathoverflow où elle a attiré les regards.

[Craw]

Ah d'accord j'avais mal compris.
Sinon c'est qui ce Bill Dubuque ? Je pourrais peut-être le contacter.

[ComeDuRondeau]

Hello,
J'ai l'impression d'avoir une preuve de ta conjecture mais si des pointures se sont cassé les dents dessus j'imagine qu'il y a une erreur quelque part.

Supposons que et que n'est pas un nombre premier. Puisque il s'agit d'un nombre impair. Supposons par l'absurde que avec et deux facteurs non triviaux, premiers entre eux (et impairs car impair). On a alors . Or pour un nombre impair on a toujours car étant donnée une écriture avec premier avec on a qui divise et est pair. Donc . Donc absurde.

En fait je pense prouver que si on définit alors implique que a au plus un facteur premier. Et ça semble impliquer la conjecture, je n'ai pas l'impression que les spécificités relatives au -ème nombre premier ou à soient utiles.

[stfj]

@ComeDuRondeau : Hello,

Pourquoi a-t-on si avec définis comme tu les définis ?



Si ce que tu affirmes est vrai, cela signifie que . Pourquoi ?

Cordialement,
Stéphane

[stfj]

[ComeDuRondeau]

@ComeDuRondeau : Hello,

Pourquoi a-t-on si avec définis comme tu les définis ?



Si ce que tu affirmes est vrai, cela signifie que . Pourquoi ?

Cordialement,
Stéphane

Toutes mes excuses, je me suis mélangé les pinceaux.
Si on écrit et on suppose que alors donc a au plus un facteur premier impair (sinon ). Donc avec premier impair et si implique ou ou et .

Donc on sait seulement que ou ou . C'est alors sûrement là que doivent intervenir les spécificités des fonctions et .

Je pense que le cas peut être écarté au moins asymptotiquement en utilisant astucieusement le théorème de raréfaction de Legendre qui dit que (je ne suis pas 100% sûr de l'équivalent qui initialement mentionne son inverse).

Pour le cas je n'arrive pas à trouver de contradiction mais j'arrive à montrer que si une telle équation est vérifiée alors ou est pair et si alors tous les sont aussi pairs. Je ne sais pas si ça peut donner des idées à quelqu'un en tout cas je n'arrive pas à éliminer ce cas.