Puissances dans C
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Jan 2012, 16:29
par Dinozzo13 » 19 Jan 2012, 16:29
Bonjour, j'aimerai savoir si ma méthode pour calculer
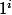
et
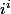
est bonne :
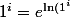}=e^{ i \ln 1}=e^0=1)
;
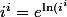}=e^{ i \ln i} =e^{i \ln\( e^{i \( \frac{\pi}{2} + 2k\pi\) } \) =e^{ - \frac{\pi}{2} + 2k\pi })
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Jan 2012, 16:32
par Nightmare » 19 Jan 2012, 16:32
Salut,
quelle est ta définition de ln(z) quand z est complexe?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Jan 2012, 16:52
par Dinozzo13 » 19 Jan 2012, 16:52
Salut Nightmare !
=\ln(|z|) +2i \arctan\(\frac{ {\rm Im}(z)}{{\rm Re}(z) + |z|}\))
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Jan 2012, 17:23
par Nightmare » 19 Jan 2012, 17:23
Et cette définition assure-t-elle que pour tout complexes a et b , ln(a^b)=bln(a) ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Jan 2012, 17:45
par Dinozzo13 » 19 Jan 2012, 17:45
Bien, je dirai que non. Mais à quoi cela m'avance-t-il ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Jan 2012, 17:47
par Nightmare » 19 Jan 2012, 17:47
Tu utilises bien cette propriété dans tes démonstrations non?
Ce que j'essaye de te faire comprendre, c'est que le log complexe est beaucoup plus délicat à manier que le log réel, pourtant, tu as faite ta manipulation comme si on était dans R.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Jan 2012, 18:25
par Skullkid » 19 Jan 2012, 18:25
J'ajouterais que ton deuxième calcul est un peu étrange, puisque tu as l'air de dire que i^i est égal à tous les
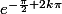
pour k entier relatif. Pourtant tous ces nombres sont différents.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Jan 2012, 19:32
par Dinozzo13 » 19 Jan 2012, 19:32
Cela vient du fait que
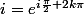}, k\in\mathbb{Z})
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Jan 2012, 19:46
par Nightmare » 19 Jan 2012, 19:46
Oui mais exp(i pi/2 + 2k pi) est constant par rapport à k, contrairement à exp(-pi /2 + 2kpi) !
Si tu écris que i^i = exp(-pi /2 + 2kpi), cela voudrait dire que i^i est égal à une infinité de valeurs...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Jan 2012, 00:56
par Dinozzo13 » 20 Jan 2012, 00:56
Donc, comment me proposeriez-vous de commencer ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 20 Jan 2012, 01:05
par Skullkid » 20 Jan 2012, 01:05
Comme l'a dit Nightmare, dans C, les logarithmes et les puissances sont délicats à définir, on est obligé de choisir une définition plus ou moins arbitraire pour faire les calculs. Apparemment tu as une définition du logarithme sous la main donc logiquement la puissance est définie à partir de ce logarithme par
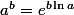
.
Après tu n'as qu'à appliquer :
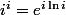
et tu calcules
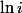
à partir de ta définition du log. En prenant une autre définition du logarithme, tu arriveras à un résultat différent.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
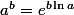 .
.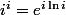 et tu calcules
et tu calcules 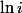 à partir de ta définition du log. En prenant une autre définition du logarithme, tu arriveras à un résultat différent.
à partir de ta définition du log. En prenant une autre définition du logarithme, tu arriveras à un résultat différent.