Puissance d'une permutation

[bourbaki]

bonjour et excellent week end à tous.
en fait, on vient de faire le cours sur les groupes symétriques et j'ai du mal à calculer la puisance de ce cycle a=(2 5 14 8 11 13). la réponse est:
a²=(2 14 11)o(5 8 13) mais j'ai pas compris la methode.pouvez vous mexpliquer les étapes du calcul??? merci
de meme b=(1 10 7) donc b²=(1 7 10) :hein: :cry: comment fait-on pour calculer tous ça??

[bourbaki]

:briques: j'ai une autre question:
pour décomposer un cycle en produit de transopsitions, comment expliquez vous le fait que:
( 1 2 3)=(1 2)(1 3)(1 2)(1 3) ??? :help:

[bourbaki]

:dingue2: :cry: alors y a personne pour m'aider :cry: :hein:

[redwolf]

Bonsoir Bourbaki.

La notation (1 7 10) désigne la permutation qui transforme 1 en 7, 7 en 10 et 10 en 1 et qui laisse tous les autres éléments inchangés.

Quand on écrit (1 7 10) (1 7 10) (ce qui est la même chose que , on compose deux fonctions. Un élément qui n'est ni 1 ni 7 ni 10 est bien sur inchangé par la composée.
Reste à calculer l'image de ces trois éléments. Je note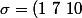 pour faire plus court. L'image de 1 par est 7 et l'image de 7 est 10. L'image de 1 par la composée est donc 10. De même, l'image de 7 par la composée est 1, et l'image de 10 est 7. En utilisant la même notation, la composée est donc la permutation (1 10 7).

D'une manière générale, quand tu écris un produit de cycles, tu calcules l'image d'un élément en regardant son image par le cycle le plus à droite, puis l'image de cette image par le cycle suivant, etc... Une fois que tu as calculé les images de tous les éléments, tu peux écrire la permutation obtenue sous forme de produit de cycles.