Puissance nième matrice

[Arayas]

Bonjour,

J'aurai besoin d'aide svp, alors je dois calculer la puissance nième de la matrice carré d'ordre 2: A=( 1 2 )
( 2 1)

je trouve A= 2B - I, avec B=(1 1) et I la matrice unité d'ordre 2.
( 1 1)
Mais lorsque j’applique la formule du binôme.
je trouve que (2B)^k est égal a 2^(2k-1) si k est non nul et égal à I si k=0
et après je bloque
Quelqu'un pourrait me débloquer svp
Merci

[GaBuZoMeu]

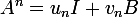
Une possibilité est de montrer que pour tout entier il existe des réels tels que , en établissant des formules de récurrence.

[mathelot]

bjr,
la matrice A est diagonalisable.
Son polynôme caractéristique est (x+1)(x-3)
Il y a donc deux valeurs propres -1 et 3 et deux vecteurs propres et

[phyelec]

Bonjour,

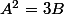
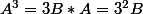
En calculant j'ai trouvé ( j'espère ne pas m’être trompé) , en calculant , si on continue on trouve une relation.

[GaBuZoMeu]

Tu t'es trompé dans tes calculs.

[phyelec]

Bonjour,
@GaBuZoMeu, oui vous avez raison. Je ne suis pas très en forme aujourd'hui. Sorry

[Arayas]

Merci infiniment à tous