Tout d'abord, bonsoir à tous et j'espère que vous serez en mesure de m'aider :
voila je cherche à déterminer la primitive de : 1/(1+x^3) ; il faudrait bien m'expliciter la démarche, j'ai passé 2 heures dessus :help:
je vous remercie par avance, et souhaite à tout le monde une excellent nuit !
Ptite question d'intégrale
4 messages
- Page 1 sur 1
Il faut commencer par décomposer en éléments simples la fraction ratinnelle 1/(1+x^3).
La DES s'écrit:
Je te laisse calculer a,b et c.
La primitive de 1/(x+1) est ln|x+1|
Pour la primitive de , il faut faire apparaître la dérivée du dénominateur au numérateur.
, il faut faire apparaître la dérivée du dénominateur au numérateur.
 où k=c-b/2.
où k=c-b/2.
La première fraction est du type u'/u et s'intégre facilement.
Pour la deuxième, il faut écrire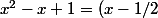^2+3/4) . En mettant en facteur 3/4, on a une fraction après changement de variable du type 1/(1+u^2) qui s'intègre en arctan(u)
. En mettant en facteur 3/4, on a une fraction après changement de variable du type 1/(1+u^2) qui s'intègre en arctan(u)
La DES s'écrit:
Je te laisse calculer a,b et c.
La primitive de 1/(x+1) est ln|x+1|
Pour la primitive de
La première fraction est du type u'/u et s'intégre facilement.
Pour la deuxième, il faut écrire
Malheureusement, il n'y a rien d'autre à faire qu'une décomposition en éléments simples.
-1 est racine de 1+x^3, et on factorise donc : 1+x^3=(1+x)(1-x+x²), avec (1-x+x²) irréductible sur R.
Donc 1/(1+x^3) s'érit sous la forme a/(1+x)+(bx+c)/(1-x+x²).
(NB : si tu ne connais pas la DES sur R, décompose sur C et regroupe les conjugués).
a/(1+x) se primitive sans problème.
Pour (bx+c)/(1-x+x²), tu fais d'abord apparaitre en haut la dérivée du bas, en faisant en sorte d'ajuster les termes en x, de sorte qu'il ne reste plus qu'une constante en terme résiduel. Concrètement, tu écris :
(bx+c)/(1-x+x²)=(b/2)(2x-1)/(1-x+x²)+k/(1-x+x²), avec k=c+(b/2). Le terme (2x-1)/(1-x+x²) se primitive alors en ln|1-x+x²|.
(NB : si b est nul, ignorer cette étape).
reste enfin le terme en k/(1-x+x^2). Tu mets le dénominateur sous forme canonique et bidouilles pour reconnaître de l'arctangente :
1/(1-x+x²)=1/((x-(1/2))²+(3/4)). On factorise le dénominateur par 3/4 :
1/(1-x+x²)=(4/3)/(1+((2x-1)/sqrt(3))²).
Une primitive en est donc (2sqrt(3)/3)arctan((2x-1)/sqrt(3)).
Bon courage pour les calculs.
-1 est racine de 1+x^3, et on factorise donc : 1+x^3=(1+x)(1-x+x²), avec (1-x+x²) irréductible sur R.
Donc 1/(1+x^3) s'érit sous la forme a/(1+x)+(bx+c)/(1-x+x²).
(NB : si tu ne connais pas la DES sur R, décompose sur C et regroupe les conjugués).
a/(1+x) se primitive sans problème.
Pour (bx+c)/(1-x+x²), tu fais d'abord apparaitre en haut la dérivée du bas, en faisant en sorte d'ajuster les termes en x, de sorte qu'il ne reste plus qu'une constante en terme résiduel. Concrètement, tu écris :
(bx+c)/(1-x+x²)=(b/2)(2x-1)/(1-x+x²)+k/(1-x+x²), avec k=c+(b/2). Le terme (2x-1)/(1-x+x²) se primitive alors en ln|1-x+x²|.
(NB : si b est nul, ignorer cette étape).
reste enfin le terme en k/(1-x+x^2). Tu mets le dénominateur sous forme canonique et bidouilles pour reconnaître de l'arctangente :
1/(1-x+x²)=1/((x-(1/2))²+(3/4)). On factorise le dénominateur par 3/4 :
1/(1-x+x²)=(4/3)/(1+((2x-1)/sqrt(3))²).
Une primitive en est donc (2sqrt(3)/3)arctan((2x-1)/sqrt(3)).
Bon courage pour les calculs.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
