Prouver une convergence normale

[ghghgh]

Bonsoir,


Soit x appartenant a [0;+oo[ . On a montré la convergence de [TEX]F(x) = \int_0{^+\infinity}e^{xt}\frac{sin(t)}{t}dt.[\TEX]

F(x) est la somme de la série de terme général [TEX]u_n(x) = \int_{n\Pi}^{(n+)\Pi}e^{xt}\frac{sin(t)}{t}dt.[\TEX]

Je dois étudier la convergence normale de la série [TEX]\sum_{n=0}{+\infinity}u_n(x)[\TEX] sur l'intervalle [0;+oo[

Mais je n'arrive pas a trouver un majorant indépendant de x qui soit sommable.

Voilà, si vous pouviez nous aider,
nous vous remercions d'avance !

[girdav]

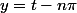
On peut faire un changement de variable du genre pour y voir plus clair dans l'intégrale.

[ghghgh]

on a bien essayé ce changement de variable, mais après lorsqu'on a essayé de majorer :
0 <= (1/n) * Int[0,Pi] (e^-(u+nPi)x) du
mais là, si on intègre on a une majoration dépendant de x, que je ne vois pas comment ôter...

[bend]

pour majorer : Un = (1/n)* Int [0,Pi]{ exp(-(u+nPi)x) du

voir que : Un = (exp(-(nPi)/x) /n) * int[0,Pi] { exp(-(u)] ]

puis


montre que au voisinage de l'infini (exp(-(nPi)/x) /n) = O (1/n²) quelque soit x

Donc au finale , montre que pour n>N0 Abs( Un) <= 1/n²
donc la serie Un converge normalement

[bend]

Donc au finale , montre que pour n>N0 Abs( Un) 0)
donc la serie Un converge normalement