Prouver que g(x+y)=g(x)+g(y) est impaire

[HelpMe11]

Bonjour,

Je bloque sur mon dm de math. Je dois prouver que :
g(x+y)=g(x)+g(y) est une fonction impaire avec (x,y) qui appartiennent aux réels.

Je sais pour le moment que g(0)=0 et g(nt)=ng(t) mais je vois pas comment utiliser cela.

Auriez-vous des pistes ? Merci

[GaBuZoMeu]

[HelpMe11]

Effectivement, on prouve que g est impaire pour g(0) mais ce n'est que un cas non ? Car x+y n'est pas tout le temps égal à 0 non ? Merci

[GaBuZoMeu]

Tu n'as apparemment pas compris mon indication.
Tu cherches à comparer g(x) et g(-x).
Prenons les choses par l'autre bout :
g(x)+g(-x) = ?

[HelpMe11]

Je pense avoir compris, cela donne donc :

g(x-x)=g(x)+g(-x)
- g(x)=g(x-x)+g(-x)
- g(x)= g(-x)

Ce qui donne ce qu'on cherche. Merci !

[HelpMe11]

Bonjour, je reposte sur le même sujet pour une autre question où je bloque sur mon dm.
Je dois prouvez que avec q qui appartient aux entiers naturels privé de 0.

Je ne vois pas du tout vers quelle direction je dois aller.

Auriez-vous des pistes ? Merci

[Sylviel]

Il faut utiliser g(n*x) = n g(x), qui s'écrit aussi g(x) = ... g(n*x).

[HelpMe11]

On a donc g(x)= 1/n*g(n*x). Il faudrait ensuite multiplier x par 1/n pour avoir le résultat voulu. Mais on ne conserve pas l'égalité ? En faites, je ne vois pas alors comment introduire le 1/n dans le g(x).

[hdci]

Bonjour,
Tu fais un changement de variable : tu poses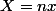 et tu récris tout avec au lieu de