Prouver qu'un nombre est entier

par **sacha.dhenin** » 25 Nov 2014, 16:06

Bonjour,

Ce théorème a l'air tout simple, et pourtant je n'arrive pas à le démontrer. Une idée ?

Voilà l'énoncé :

si

, alors

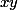
est un carré parfait.

J'ai tenté de tout élever au carré, mais je n'arrive qu'à montrer que

est un entier, pas plus.

Merci d'avance pour votre aide !

par **arnaud32** » 25 Nov 2014, 16:11

et

entiers et

premiers >2
...

par **chan79** » 25 Nov 2014, 17:18

donc

avec p entier

si

est pair,

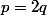
avec

entier

si

est impair,

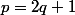
impossible car 1 serait pair

par **sacha.dhenin** » 26 Nov 2014, 05:12

Merci à tous les deux ! C'est clair, maintenant ! :)