Propriétés fonction associée

[yoyo07]

Bonsoir à tous,

J'ai un exercice qui consiste à indiquer si chaque affirmations sont vraie ou fausse. Certaines propositions m'ont parût tout de suite vraies (ou fausses), cependant je bloque encore sur 3 affirmations :

Sujet : soit une suite définie par où est donné.

Propositions :
- Si la suite est croissante, la fonction f est croissante. VRAIE
- Si la suite est décroissante et la fonction f est monotone, alors f est croissante (Faux ?)
- Si la fonction f est croissante et , la suite est décroissante (FAUX ?)
- Si la fonction f est croissante, la suite est monotone (je ne sais pas du tout)
- Si la fonction f est décroissante et , la suite est décroissante (VRAIE)

Merci par avance pour votre aide.

[Skullkid]

Bonsoir, les bonnes réponses sont

- Si la suite est croissante, la fonction f est croissante. FAUX
- Si la suite est décroissante et la fonction f est monotone, alors f est croissante. FAUX (en revanche ça devient vrai si on précise que la suite est strictement décroissante, donc "vrai" est peut-être la réponse attendue...)
- Si la fonction f est croissante et , la suite est décroissante. VRAI
- Si la fonction f est croissante, la suite est monotone. VRAI
- Si la fonction f est décroissante et , la suite est décroissante. FAUX

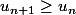
Pour comprendre pourquoi, on peut écrire en détail ce que chaque proposition signifie. Par exemple pour la première, dire que la suite est croissante signifie que pour tout n, , c'est-à-dire que pour tout n, . Ne peux-tu pas trouver une fonction f, qui ne soit pas croissante, mais qui permette de vérifier à coup sûr cette inégalité ?

[Tiruxa47]

Bonjour,

Pour illustrer, un contrexemple parmi d'autres de la première proposition.
f définie sur R par :
f(x)=x+3+2sinx

En encadrant le sinus on voit que f(x)> x pour tout réel x, donc (Un) est strictement croissante

Or la dérivée de f, f'(x)=1+2cosx change de signe pour tout x tel que cos x=-0.5
donc f n'est pas monotone