Propriétés des racines d'un polynôme de degré n.

[Dalem116]

Bonjour à vous! J'espère que mon sujet se trouve au bon endroit, étant donné que je suis québécois, je ne suis pas absolument certain mais bon, allons-y!

Je m'interroge sur une formule que je suis en train de voir au niveau de la factorisation des polynômes de degré supérieur à 2. Je ne comprend pas comment le symbole de double sommation peux s'appliquer ici..

Merci!

[Pythales]

[Lostounet]

Bonjour Dalem, et bienvenue sur notre forum

Le problème initial est de trouver un polynôme de degré 3 de racines 3, -4 et 5.
Notons ces racines , 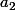et 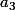. On peut considérer le polynôme:

Développons ce polynôme et regroupons les termes de même degré:



Tes sommes et produits traduisent exactement ce développement. Je pense que tu comprends la 1ere somme, qui te dit que l'opposé du coefficient devant x^2 est

Le troisième symbole 'pi' est le produit des trois racines multiplié par (-1)^degré du polynôme (formule du cours) qui est bien le terme "a0" la constante que l'on voit apparaitre tout à droite.

En ce qui concerne la double somme du milieu, c'est simple: tu commences par la somme de gauche. Tu lis j = 1 puis k > j donc k > 1 il faut donc faire a_j = a1 fois (a2 + a3) (on prend les termes avec un indice supérieur à j = 1)
Plus (j = 2) a_j = a_2 fois (a_3) (on prend les termes avec un indice supérieur à j = 2)
Plus (j = 3) a_3 fois (rien du tout car il y a pas de termes ici d’indice > 3 !) = 0

Finalement, c'est la somme et c'est bien le coefficient devant le terme "x" donc le coefficient a1

Pour conclure, il suffit donc tout simplement de remplacer a1 et a2 et a3 par leurs valeurs imposées ou sinon tu peux développer