Proposition géométrique à prouver

[brice.michoud]

Bonjour.
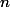
Je me place dans le contexte de la visibilité de points par un ensemble de caméras
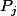
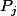
Soient un point de , et le nombre de caméras dans lequelles est visible.
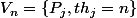
soient et
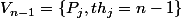
Voici la proposition qui pose problème:

Si et Alors est connexe.
image d'exemple
Dans cet exemple la partie gris foncé représente $V_n$ et la partie claire $V_{n-1}$

Je n'arrive par à réaliser la preuve de cette proposition

Si vous pouviez m'aider....

Merci

[brice.michoud]

Si quelqu'un est intéressé par la preuve, dites le moi dans ce post..

Bonne journée

[yos]

J'ai pas eu le temps d'y réfléchir, mais c'est un beau problème. Je veux bien la preuve ou les idées au moins. Merci.

[zorg]

Ton problème est intéressant. Au début je pensais raisonner par récurrence. Mais il me semble qu'une preuve directe est possible.

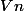
Si j'ai bien compris l'énoncé, est la région du plan où les points sont vus EXACTEMENT par n projecteurs.

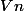
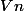
Tout d'abord chaque est convexe car c'est l'intersection de parties convexes donc chaque est connexe.

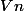
Le point central que je n'arrive pas à formaliser c'est que l'intersection de et est non vide. Ca semble évident sur un dessin...

Dans ce cas, l'union est connexe.

Je suis intéressé par la preuve et aussi l'application pratique (la surveillance d'un centre commercial ? ou d'une bijouterie ?)

[yos]

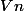
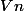
Tout d'abord chaque est convexe car c'est l'intersection de parties convexes donc chaque est connexe.

Les Vn ne sont pas convexes ni même connexes en général.

[brice.michoud]

Les caméras sont représentées par un ensemble de cônes ou de pyramides qui sont par définition des convexes dans .
L'intersection de convexes non vides est convexe, donc connexe.

Je vous écrit la suite dans pas longtemps.

[yos]

Il doit manquer une hypothèse dans ton truc. Prends le cas de deux caméras "dos à dos" : les cônes ont des sens opposés ( exemple : > < ). V0 et V1 sont non vides, non convexes, non connexes.

On peut même aller plus loin : imagine 4 caméras aux sommets d'un carré. On suppose que les caméras sur le côté nord du carré ont l'axe de leur cône dirigé vers le nord et les caméras sur le côté sud du carré ont l'axe de leur cône dirigé vers le sud. Désolé j'ai pas envie de faire le dessin. On a ici V1 et V2 non vides et non connexes de même que V1 U V2.