Proposer une base de ker(f) et Im(f)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 11 Déc 2013, 15:00
par psp » 11 Déc 2013, 15:00
Bonjour,
Soit E =
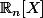
et

tel que f : P -> P + (1-X)P'
Je dois proposer une base de Ker(f) et de Im(f)
Je pose P =

Je tombe enfin sur :
f(P) =
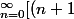a_{n+1} + (1-n)a_{n}]X^{n})
Pour ker(f) j'ai donc supposé f(P)=0
Par conséquent

Par récurrence pour

on a :
})
Avec

Maintenant est ce que ker (f) =
}X^{n})
ça j'en sais rien... maintenant pour déterminer Im(f) je ne sais pas comment procéder !!
mes bases en algèbre linéaire sont très fragiles, on en fait cette année mais aucun rappel n'a été fait et l'année d'avant je n'en avais jamais fait.
Si quelqu'un peut m'apporter son aide....merci

)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 11 Déc 2013, 15:32
par arnaud32 » 11 Déc 2013, 15:32
quelle est la dimension de ker(f)?
peux tu donner a1? a2? a3?
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 11 Déc 2013, 15:38
par psp » 11 Déc 2013, 15:38
Peut être n, j'en sais rien, si tu as un source de cours spécifique où un exercice similaire corrigé ça m'aidera énormément, par ce que l'algèbre linéaire c'est tellement pas naturel pour moi on pourrais jouer aux devinettes pendant 9 semaines
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 11 Déc 2013, 15:40
par arnaud32 » 11 Déc 2013, 15:40
avec ta relation tu as
a1=-a0
a2=0
et donc ak=0 pour k>1
ce qui signifie que P(X)=a0*(1-X)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 11 Déc 2013, 15:51
par arnaud32 » 11 Déc 2013, 15:51
pour la suite ce que je te propose c'est de calculer
^k ))

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2013, 15:52
par Ben314 » 11 Déc 2013, 15:52
Salut tout le monde.
Au cas où tu ait déjà vu la notion, je signale juste que P+(1-X)P'=0, ça porte un nom : ça s'appelle... une équation différentielle...
Et je pense que ça va plus vite de la résoudre une bonne fois pour toute (dans l'ensemble des fonction C^1 sur un intervalle à déterminer) PUIS de regarder quelles sont les solutions polynômiales.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 11 Déc 2013, 16:46
par psp » 11 Déc 2013, 16:46
Merci donc le noyau de f est un espace vectoriel de dimension 1 et on a un vecteur directeur le polynome X-1.
Je me débrouillerai pour Im(f) merci !
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 11 Déc 2013, 20:13
par psp » 11 Déc 2013, 20:13
Pour une base de Im(f) j'ai trouvé
{
,f(X^{2}),...,f(X^{n}))
}
Vérifiez si vous le souhaitez

)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2013, 21:40
par Ben314 » 11 Déc 2013, 21:40
psp a écrit:Pour une base de Im(f) j'ai trouvé
{
,f(X^{2}),...,f(X^{n}))
}
Vérifiez si vous le souhaitez

)
C'est bon vu que
,f(X),f(X^2),...,f(X^n)\})
est (presque par définition) une famille génératrice de Im(f) et qu'on sait aussi que Im(f) est de dimension n-1 donc dans cette famille, il faut enlever un vecteur pour avoir une base.
Reste à vérifier qu'en enlevant (par exemple) f(1) la famille devient libre, mais en fait ça vient du fait que le s.e.v. engendré par

(on a enlevé 1) ne rencontre ker(f) qu'en {0}.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
