Lostounet a écrit:Sur l'intervalle que décrit t non? ] alpha; beta[
Surement pas.
Tout ce que tu sait, c'est que,
si pour un certain
on a
\!=\!1)
alors
\!<\!0)
.
Au mieux, et en utilisant la continuité de

, ça prouve que

est décroissante sur un petit intervalle ouvert contenant
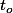
, mais on a même pas besoin de ça.
Ce truc est contradictoire du fait que, si

prenait au moins une fois une valeur
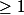
pour
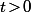
alors
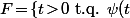\!\geq\!1\})
serait une partie non vide de
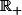
donc admettrais une borne inf
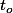
qui vérifierais évidement
\!=\!1)
(donc

) mais aussi
\!\geq\!0)
vu que si

alors

donc
\!<\!1\!=\!f(t_o))
)
Bref, une fonction dérivable qui part en dessous de la droite y=1 et qui n'a le droit de couper cette droite que de "haut en bas" (i.e. avec une dérivée <0), ben c'est qu'elle la coupe jamais et donc qu'elle reste toujours en dessous.
Lostounet a écrit:Mais cela ne contredit-il pas le lemme "d'explosion des solutions" en dimension finie ?
a) Je sais pas ce que c'est ton théorème.
b) Je ne pense pas qu'il y ait un quelconque rapport avec la choucroute vu que les seul arguments utile ici, c'est de la bête analyse à deux sous de fonction dérivable de R->R.
