Prolongation en une fonction de classe C1
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
flocaz
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Sep 2006, 10:03
-
par flocaz » 29 Jan 2009, 16:12
Bonjour à tous
j'ai une fonction
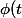=\frac{1}{t} - \frac{1}{sin(t)})
. Je dois prouver qu'elle est prolongeable en une fonction
sur
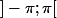
Le souci est donc en 0, je fais mon dl, je montre que c'est prolongeable, pas de problème.
Mais je ne sais pas comment justifier qu'elle est dérivable, ( de manière à faire la même chose pour la dérivée) y compris en 0 ?
Merci de votre aide !!
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
par L.A. » 29 Jan 2009, 16:24
Bonjour.
la fonction est C1 sur I = ]-pi, 0[U]0, pi[. on la prolonge en une fonction C0 sur J= ]-pi, pi[.
si la dérivée (définie sur I) admet une limite quand x en 0, alors la fonction prolongée est automatiquement C1 sur J, et la valeur de la dérivée en 0 est la limite.
-
flocaz
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Sep 2006, 10:03
-
par flocaz » 29 Jan 2009, 16:38
en fait, après avoir prolongé ma fonction en 0, je calcule la dérivée sur I ( et pas sur I U {0} ), et le fait que le dl de cette dérivée admette une limite finie en 0 justifie sa dérivabilité sur I U {0} ?
rien de plus à préciser ?
merci beaucoup !
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
par L.A. » 29 Jan 2009, 17:22
oui.
la démonstration utilise la formule de Taylor Lagrange, ou du genre...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
