Projet methode de point fixe pour polynome quadratiques
13 messages
- Page 1 sur 1
Bonjour, et bienvenu sur le forum !
Pour répondre à la deuxième question, imagine que, dans le plan complexe, on dessine en rouge tous les points d'affixe tels que la suite
tels que la suite ) tende vers l'infini et en vert tous les autres.
tende vers l'infini et en vert tous les autres.
Alors, ton ensemble de Julia rempli est colorié en vert. Et l'ensemble de Julia est la frontière entre le vert et le rouge.
On te signale à un moment que si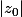 est assez grand, on est colorié en rouge. L'ensemble de Julia rempli (en vert) est donc à chercher près de l'origine.
est assez grand, on est colorié en rouge. L'ensemble de Julia rempli (en vert) est donc à chercher près de l'origine.
Pour répondre à la deuxième question, imagine que, dans le plan complexe, on dessine en rouge tous les points d'affixe
Alors, ton ensemble de Julia rempli est colorié en vert. Et l'ensemble de Julia est la frontière entre le vert et le rouge.
On te signale à un moment que si
Ce sont les propriétés qui dépendent d'un entier naturel n qu'on peut démontrer par récurrence...
Je te donne des questions intermédiaires très détaillées:
1. On pose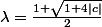 . Montrer que
. Montrer que  est un point fixe de
est un point fixe de  , i.e.
, i.e. =\lambda) .
.
2. Montrer que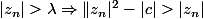 quel que soit
quel que soit  .
.
3. Justifier que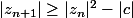 .
.
4. Montrer que s'il existe m tel que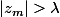 , alors on a
, alors on a 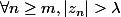 .
.
4. Montrer que(|z_{n}|-\lambda)) .
.
5. Conclure.
Cette propriété démontre deux choses:
*Que l'ensemble de Julia rempli est effectivement à l'intérieur du disque de centre 0 et de rayon (comme on te l'avait annoncé);
(comme on te l'avait annoncé);
*Que dès qu'un terme de la suite) est hors de ce disque, on est certain que le
est hors de ce disque, on est certain que le  n'appartient pas à l'ensemble de Julia rempli. On peut donc arrêter l'algorithme lorsqu'on fait une recherche informatique.
n'appartient pas à l'ensemble de Julia rempli. On peut donc arrêter l'algorithme lorsqu'on fait une recherche informatique.
Je te donne des questions intermédiaires très détaillées:
1. On pose
2. Montrer que
3. Justifier que
4. Montrer que s'il existe m tel que
4. Montrer que
5. Conclure.
Cette propriété démontre deux choses:
*Que l'ensemble de Julia rempli est effectivement à l'intérieur du disque de centre 0 et de rayon
*Que dès qu'un terme de la suite
Va faire un tour sur l'excellent site MathCurves pour avoir une idée de quelques ensembles de Julia remplis...
boucblond a écrit:il faudrait que l'on ait Zn+1>Zn
Un peu de sérieux... Des complexes plus grands que d'autres ?
Et même si tu avais écrit
Ma dernière indication : les suites géométriques, cela te dit quelque chose ?
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
