Projection orthogonal sur Vect((1,...,1))
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 19 Jan 2019, 17:08
par fioldodidi » 19 Jan 2019, 17:08
Bonjour,
Quelqu'un pourrai m'aider à trouver la projection orthogonal d'un vecteur quelconque :

sur
)
avec
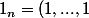^T \in R^n)
?
Je vois ce que cela veux dire dans l'espace mais je comprend pas comment caractériser
)
mathématiquement.
Merci


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Jan 2019, 19:40
par Ben314 » 19 Jan 2019, 19:40
Salut,
C'est toujours la même méthode (axée bien sûr sur la définition d'une projection) :
Pour trouver le projeté orthogonal de ton vecteur

sur une droite vectorielle
)
(avec

vecteur non nul connu), il faut arriver à l'écrire
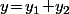
avec
)
et
^{\perp})
.
Sauf que dire que
)
ça signifie que
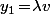
pour un certain

et dire que
^{\perp})
ça signifie que
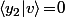
(produit scalaire). Or on doit avoir
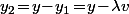
donc en fait il faut que
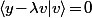
c'est à dire
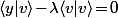
soit encore
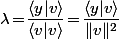
(on a
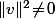
vu que

est non nul)
Bilan : le projeté orthogonal de

sur
)
est
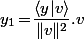
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 19 Jan 2019, 21:54
par fioldodidi » 19 Jan 2019, 21:54
Merci !
Donc avec
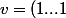^T)
on :
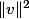
= 1
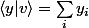
donc
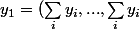^T)
C'est bien ça ?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 20 Jan 2019, 10:40
par pascal16 » 20 Jan 2019, 10:40
||(1,1,1,1,.)||² = 1+1+1 ...1 = n
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 20 Jan 2019, 13:22
par fioldodidi » 20 Jan 2019, 13:22
Oups merci :
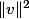
= n
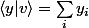
donc
 = (\sum_i y_i/n, ..., \sum_i y_i/n)^T)
Donc chaque coordonnées de
)
est la moyenne de

, est-ce que cela à une signification particulière ?
Merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités