Projectifs

[kagoune]

j'ai l'application

F:P(R²) -> R U {inf} : [x:y] -> x/y si y<> 0 et inf si y=0

il faut montrer qu'elle est bijective?
merci

[yos]

Bonjour.
Faut juste remonter ses manches .
Injectivité :
la classe de (1,0) est le seul antécédent de .
Si x/y=x'/y', alors
- soit x=0, et alors x'=0 et [x,y]=[x',y'],
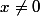
- soit et alors x'/x=y'/y ce qui montre que [x,y]=[x',y'].

Surjectivité : je te laisse regarder.

[yos]

C'est quoi P(R²) parce que si c'est R² tout entier c'est pas vrai.

C'est le plan projectif (quotient de R²-{(0,0)} par la relation d'équivalence (x,y)R(x',y') ssi il existe k tel que (x',y')=k(x,y).)

[abcd22]

C'est le plan projectif (quotient de R²-{(0,0)} par la relation d'équivalence (x,y)R(x',y') ssi il existe k tel que (x',y')=k(x,y).)

La droite projective plutot :we:
Interpretation geometrique de l'application : si [x:y] correspond a la droite d'equation xX + yY = 0 dans (pas super comme notations mais bon), x/y est l'ordonnee du point d'intersection de cette droite avec la droite d'equation X = -1, si on voit la droite projective comme l'ensemble des droites (lineaires) du plan on voit tout de suite que chaque droite (lineaire) a un point d'intersection unique avec la droite affine d'equation X = -1, sauf celle d'equation X = 0 qui correspond au point [1:0] de la droite projective et donne le point a l'infini.

[kagoune]

merci pour la réponse, je sais pas pourquoi je trouvais ça faux quand je fesait la surjectivité.. enfin normalemen c'est bon! merci
Par contre je ne comprends pas une question:
"comment le groupe PGL(R²) agit-il sur R U {inf}?"
je ne sais pas du tout qu'est ce qu'il faut que je réponde.... :triste:

[yos]

La droite projective plutot

mea culpa.

Pour l'autre question, GL(R²) agit sur R² et induit via la bijection précédente l'action de PGL(R²) sur .