Produit transformée de Laplace

[jikoloko]

Bonsoir,

Je solliciterais bien votre aide pour le calcul suivant.
Calculer la transformée de Laplace de

Bon d'après les transformées usuelles, j'ai

d'où


Cependant je ne vois pas comment les utiliser pour trouver la transformée de Laplace du produit 2cos(4t)exp(-3t).

Je vous remercie d'avance.

[cuati]

Bonsoir, tu as quasiment terminé...
utilise la définition :

[jikoloko]

Eh bien, merci beaucoup ;)
Bonne soirée.

[jikoloko]

Hm... désolé, j'ai un petit problème sur la dernière question:
Calculer dx(t)/dt. En déduire dx(0+)/dt et vérifier le résultat par le théorème de la valeur initiale.

Donc je dérive x(t)=2cos(4t)exp(-3t)

je pose u(t)=2cos(4t) v(t)=exp(-3t)
u'(t)=-8sin(4t) v'(t)=-3exp(-3t)

d'où x'(t)=-8sin(4t)exp(-3t) -6cos(4t)exp(-3t)
x'(t)=-exp(-3t)(8sin(4t)+6cos(4t))

je trouve dx(0+)/dt=-6.

Mais je ne vois pas trop comment vérifier le résultat par le théorème de la valeur initiale.
Dois-je vérifier lim p.L(x)(p) quand p tend vers l'infini?

[cuati]

En utilisant la formule de la transformé de Laplace d'une dérivée :


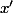
Pour utiliser le théorème de la valeur initiale appliqué à , on calcule la limite quand p tend vers l'infini de :
il reste à mettre au même dénominateur et calculer la limite... qui vaut bien -6.


[Edit] Tiens ?! Ta dernière question a été supprimée...

[jikoloko]

Oui je suis désolé, je venais de trouver la réponse et ne voulais pas vous importuner, mais vous avez été plus rapide. En tout cas je vous remercie pour votre aide.