Produit de sinus

[Aspx]

Bonjour !

Est-il possible de calculer les produits suivants :

ou

Merci d'avance.

[tize]

Bonjour,
je pense que tu as oublié des k...

[Clembou]

Bonjour !

Est-il possible de calculer les produits suivants :

ou

Merci d'avance.

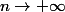
Si tu connais la valeur de , tu m'appelles :marteau: Non sérieusement, si alors

[Aspx]

oui excuse moi il faut remplacer le n du produit par un k.
ou

[Aspx]

Si tu connais la valeur de , tu m'appelles :marteau:

se calcule en itérant la formule si je ne me trompe pas.

Pourquoi ?

[ThSQ]

Le deuxième est facile, il suffit d'itérer la formule donnant sinx/2.

[Aspx]

Excusez moi je suis vraiment pas en forme ce soir.

Rectification :



Bien moins trivial...

[ThSQ]

Lol, bon on va attendre que tu sois vraiment vraiment sûr de la formule :lol5:

[Aspx]

Le but de mon exercice est de calculer
[CENTER][/CENTER]

Pour cela on cherche une méthode alternative à la méthode classique astucieuse qui consiste à écrire que c'est pareil qu'avec le cosinus puis faire la somme, changement de variable & co (la valeur cherchée est d'ailleurs )

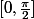
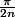
Pour cela on utilise le fait que est croissante sur puis on encadre des intégrales partielles de notre choix (d'où la discussion entre et ). Après calcul on arrive à encadrer nos intégrales partielles entre deux sommes de logarithmes, i.e le logarithme d'un produit, le produit que je vous présente. L'idée serait donc d'en trouver la limite (et il semblerait que ce soit )

Voilà voilà...

[ThSQ]

Ah ok ben c'est tout bête avec des sommes de Riemann ...


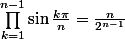
qui se voit en regardant les racines de

[Aspx]

Merci beaucoup ThSQ, j'avais fait un mauvais découpage, on tombe en effet sur des sommes de Riemann.

Par contre moi j'ai je vais vérifier mon calcul.

[Aspx]

J'ai l'encadrement suivant :
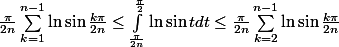
[CENTER][/CENTER]
Puis
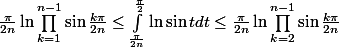
[CENTER][/CENTER]

[ThSQ]

Pas compris pourquoi tu veux encadrer ni comment tu obtiens du 1/2n mais c'est pas grav' :briques:

[Aspx]

@ ThSQ : c'est une intégrale impropre, c'est pourquoi on cherche la limite de certaines de ses intégrales partielles en les encadrant.

[ThSQ]

Ok mais dans le cas où la fonction est monotone (et C°) ça marche, on peut prendre la limite des sommes de Riemann.

[Aspx]

En quoi la monotonie a à voir avec les sommes de Riemann ? Il faut juste être capable d'appliquer Heine sur chaque segment pour une fonction continue sur .

[ThSQ]

En quoi la monotonie a à voir avec les sommes de Riemann ?

Si tu relisais le thread au lieu d'envoyer péter ceux qui tentent de t'aider (maladroitement à ton gout semble-t-il) tu verrais qu'il s'agit d'intégrales impropres pour lesquelles les sommes de Riemann sont à manipuler avec prudence (sauf dans le cas où la fonction est monotone par ex.).

[Aspx]

Si tu relisais le thread au lieu d'envoyer péter ceux qui tentent de t'aider (maladroitement à ton gout semble-t-il) tu verrais qu'il s'agit d'intégrales impropres pour lesquelles les sommes de Riemann sont à manipuler avec prudence (sauf dans le cas où la fonction est monotone par ex.).

Désolé c'était pas vraiment mon but.
Mon exercice me demande explicitement d'encadrer les intégrales partielles par des sommes de Riemann, mais si on peut le faire plus trivialement en l'interprétant comme la limite de la somme de Riemann associée (qui fait intervenir ton produit je suis d'accord et donne la bonne limite) pourquoi pas !

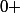
C'est le fait que l'intégrande n'ai pas de limite finie en qui me tracasse pour exprimer l'intégrale comme limite d'une somme de Riemann. Comment montrer que ça reste valable vu la monotonie ?